[Guilherme Parreira] | June 8, 2018
Olá pessoal, tudo bem?
Nesse post irei tratar de uma distribuição de probabilidade que não é muito conhecida, a distribuição Tweedie. A distribuição Tweedie é uma família de distribuições de probabilidade, em que a normal, gamma, normal inversa, Poisson e Poisson-gamma composta são casos particulares dela. Ela não possui forma fechada, no entanto, ela pertence a classe da família exponencial, sendo assim, é possível utilizar tal distribuição no contexto dos modelos lineares generalizados (GLM).
Caracterização da distribuição Tweedie
O domínio da distribuição Tweedie é dos números reais positivos com o zero (\(R_{+} = 0, ..., \infty\)), e é utilizada para modelar (acomodar) variáveis que possuem comportamento assimétrico. O fato da Tweedie permitir que a variável aleatória assuma valor 0 garante uma vantagem em relação as demais distribuições que comportam variáveis assimétricas, como a gamma e normal inversa, pois as mesmas não possuem tal flexibilidade.
A distribuição Tweedie é representada pelos dois primeiros momentos amostrais, isto é, a média (\(\mu\)) e a variância (\(V\)). Seja \(Y\) uma variável aleatória com distribuição Tweedie, a média e a variância de Y podem ser escritas respectivamente por:
\[E (Y) = \mu\] \[V(Y) = \phi V(\mu) = \phi\mu^p\]
A esperança da variável aleatória Y é igual ao parâmetro \(\mu\), ou seja, é não viciado, e pode ser estimado pela média amostral (\(\bar{Y}\)). Já V(Y) depende do parâmetro de dispersão (\(\phi\)), potência (\(p\)) e da média (\(\mu\)): é aqui que a distribuição ganha em flexibilidade e a capacidade de acomodar diferentes distribuições. Nota-se que essa dependência é em relação ao parâmetro \(p\), que controla quão grande é a dependência da variância em detrimento da média: quanto maior o \(p\) maior é a dispersão dos dados. Dado alguns valores de p, algumas distribuições de probabilidade são definidas:
| p | Distribuição.de.Probabilidade |
|---|---|
| p = 0 | Normal |
| 0 < p < 1 | Não existe distribuição Tweedie via ML* |
| p = 1 | Poisson |
| 1 < p < 2 | Poisson-gamma composta (aceita dados frequência no 0) |
| p = 2 | Gamma |
| 2 < p < 3 | Positivas estáveis |
| p = 3 | Inversa Gaussiana |
| p > 3 | Positivas estáveis |
| p = \(\infty\) | Positivas extremas |
Por exemplo, ao utilizar a distribuição Tweedie, e obter um valor de \(p\) próximo a 0, têm-se indícios de que a variável resposta em questão assume distribuição Normal. Estimação de \(p\) pelo método da máxima verossimilhança (\(ML\)) não permite que o valor de p varie entre 0 e 1 (pois para 0 < p < 1, quando \(E[Y] \rightarrow \infty \therefore V[Y] \lt 0\)). Ao estimar o \(p\) via quase-verossimilhança, tal valor é possível, uma vez que tal estimação não assume uma forma específica da densidade dos dados.
Relação média variância
A tabela anterior apresentou a relação média e variância da distribuição Tweedie. Essa seção irá ilustrar como funciona essa relação entre os dois momentos amostrais através de um estudo teórico e outro por simulação.
Estudo teórico da relação média variância
Em um primeiro momento, simplesmente iremos estudar a relação teórica entre \(V[Y]\) e \(E[Y]\). Para isso, basta estabelecer um grid de valores para \(E[Y]\) e exponenciar tais valores de acordo com o parâmetro de potência (\(p\)). Para tal exemplo, iremos utilizar:
- \(E[Y]\) = 10, 11, 12, …, 100;
- \(p\) = 0, 1, 1.5 e 2;
- \(\phi = 1\)
Não será utilizado \(p\) = 3 por conta da escala, que dificulta avaliar a relação média-variância das demais distribuições através de gráfico.
# Teórico
means <- 10:100
df <- data.frame(p0 = means^0,
p1 = means,
p1.5 = means^1.5,
p2 = means^2,
means = means)
df.l <- reshape2::melt(df, id.vars = "means")
levels(df.l$variable) <- c("p = 0 (normal)", "p = 1 (Poisson)", "p = 1.5 (Poisson-gamma)", "p = 2 (gamma)")
df.l$value.s <- sqrt(df.l$value)
df.l$means.s <- sqrt(df.l$means)
# Raiz quadrada no braço
g0 <- ggplot(data = df.l, aes(x = means.s, y = value.s, colour = variable)) +
geom_line() +
labs(x = expression(sqrt("E[Y]")),
y = expression(sqrt("V[Y]")),
title = "Relação média e variância teórico") +
scale_y_continuous(breaks = c(0, 4, 6, 8, 10, 25, 31.6, 50, 75, 100, 105))Estudo de simulação da relação média e variância
Para o estudo de simulação serão mantidos os mesmos valores de parâmetros do estudo teórico. Para cada valor de \(E[Y]\) e \(p\) foram gerados 10000 valores de cada uma das distribuições já comentadas, e calculado a \(V[Y]\). Para \(p = 0\) os dados foram gerados a partir da função rnorm, para os demais valores de \(p\), foi utilizado a função tweedie::rtweedie. A função tweedie::rtweedie não aceita valor de \(p = 0\); para \(p = 1\) ela utiliza a função \(rpois\) e para \(p = 2\) ela utiliza a função \(rgamma\). Por mais que utilizamos tweedie::rtweedie, o que de fato acontece, é que ela é um wrapper para as demais funções base do R, possibilitando assim que a simulação seja mais rápida, e ela é de fato “utilizada” quando \(p > 2\) e \(1 < p < 2\) (porém, é lenta).
Os gráficos abaixo ilustram a relação média variância para o estudo teórico e via simulação:
means <- 10:100
lmean <- length(means)
ps <- c(0, 1, 1.5, 2)
lp <- length(ps)
df <- data.frame(p0 = numeric(lmean),
p1 = numeric(lmean),
p1.5 = numeric(lmean),
p2 = numeric(lmean),
means = means)
for(i in 1:lmean){
for(j in 1:lp){
if(ps[j] == 0){
df[i, j] <- var(rnorm(10000, mean = means[i], sd = 1))
} else{
df[i, j] <- var(tweedie::rtweedie(10000, power = ps[j], mu = means[i], phi = 1))
}
}
}
df.l <- reshape2::melt(df, id.vars = "means")
df.l$value.s <- sqrt(df.l$value)
df.l$means.s <- sqrt(df.l$means)
g1 <- ggplot(data = df.l, aes(x = means.s, y = value.s, colour = variable)) +
geom_line() +
labs(x = expression(sqrt("E[Y]")),
y = expression(sqrt("V[Y]")),
title = "Relação média e variância simulado") +
scale_y_continuous(breaks = c(0, 4, 6, 8, 10, 25, 31.6, 50, 75, 100, 105))
ggpubr::ggarrange(g0, g1, ncol = 2, nrow = 1, common.legend = TRUE, legend = "bottom")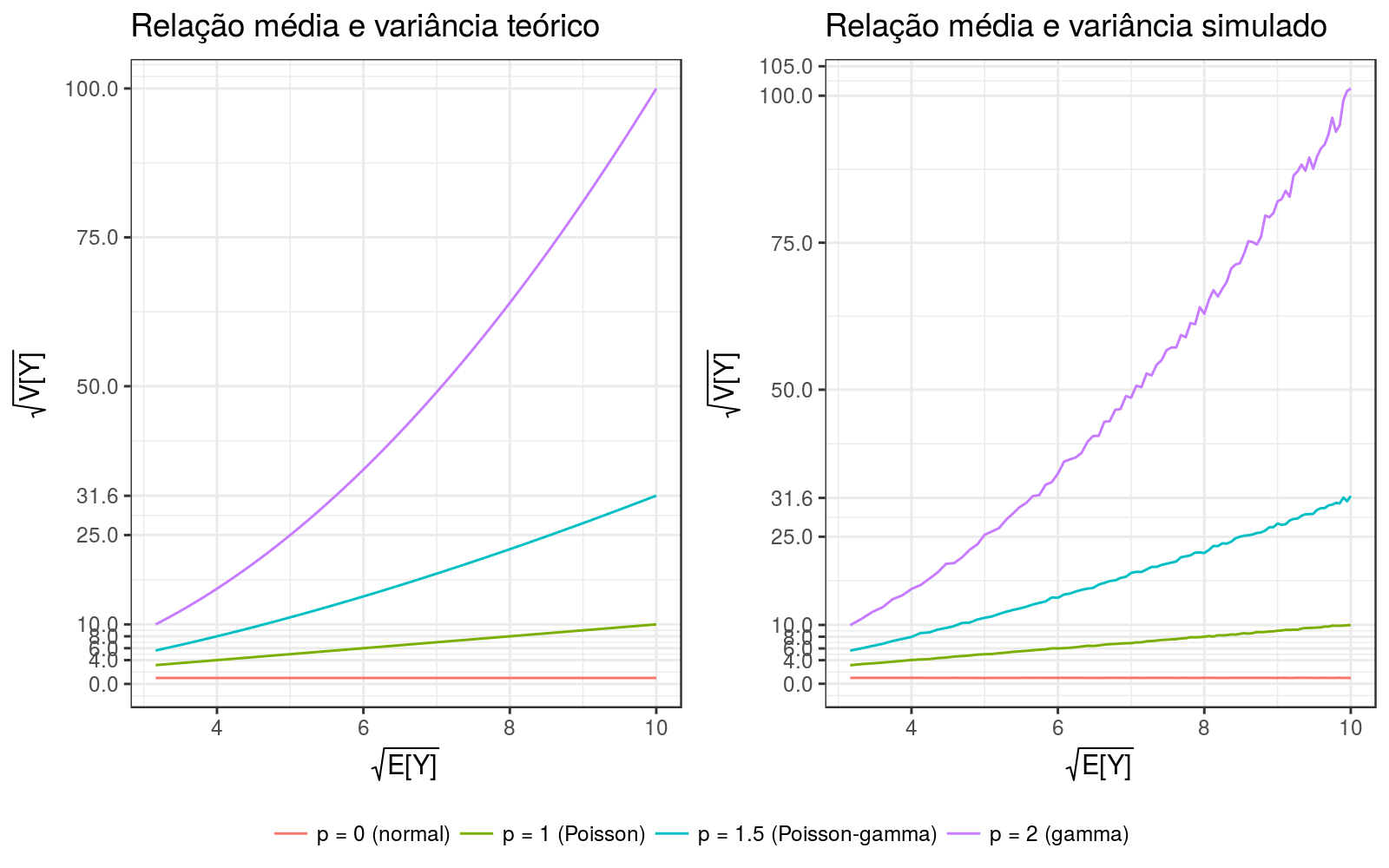
Nota-se que ambos gráficos comportam-se de maneira similar. Para ambos os eixos foi aplicada a transformação da raiz quadrada para melhor visualizar as curvas. Segue interpretação para cada valor de \(p\)
- Para \(p = 0\) a variância constante conforme a média aumenta;
- Para \(p = 1\) os valores da variância são iguais aos valores da média;
- Para \(p = 1.5\) os valores da variância aumentam mais rapidamente que a média;
- Para \(p = 2\) os valores da variância são bem mais acentuados que os valores da média;
Para melhor entender tal relação, pegue os valores do eixo x, e os exponencie de acordo com o valor de p da correspondente curva: o valor encontrado deve corresponder ao valor do eixo Y.
Forma da densidade
Uma vez que já entendemos a relação média variância, estudaremos a forma da curva da distribuição Tweedie, isto é, a sua densidade. Para tal, calcularemos o valor da densidade da distribuição Tweedie via tweedie::dtweedie (e quando \(p = 0\) utilizaremos dnorm) fixando \(\mu = 10\), dispersão (\(\phi = 3\)) e Y limitado a 60. Aqui incluímos a distribuição Normal Inversa e removemos a Poisson (pois não é contínua). A próxima figura apresenta a comparação das 4 distribuições:
end <- 80
mean <- 10
phi <- 2
a <- curve(dnorm(x, mean = mean, sd = phi), from = -3, end)
b <- curve(dtweedie(x, power = 1.5, mu = mean, phi = phi), from = 0,to = end, col = "purple", add = T)
c <- curve(dtweedie(x, power = 2, mu = mean, phi = phi), from = 0.01,to = end, col = "red", add = T)
d <- curve(dtweedie(x, power = 3, mu = mean, phi = phi), from = 0.01,to = end, col = "blue", add = T)
a$y <- a$y/max(a$y)
b$y <- b$y/max(b$y)
c$y <- c$y/max(c$y)
d$y <- d$y/max(d$y)
plot(a, type = "l", ylab = "Densidade", xlab = "Y")
legend("topright",
col = c("black", "purple", "red", "blue"),
legend = c("p = 0 (normal)", "p = 1.5 (gamma-Poisson)","p = 2 (gamma)", "p = 3 (normal inversa)"),
lty = 1)
lines(b, col = "purple")
lines(c, col = "red")
lines(d, col = "blue")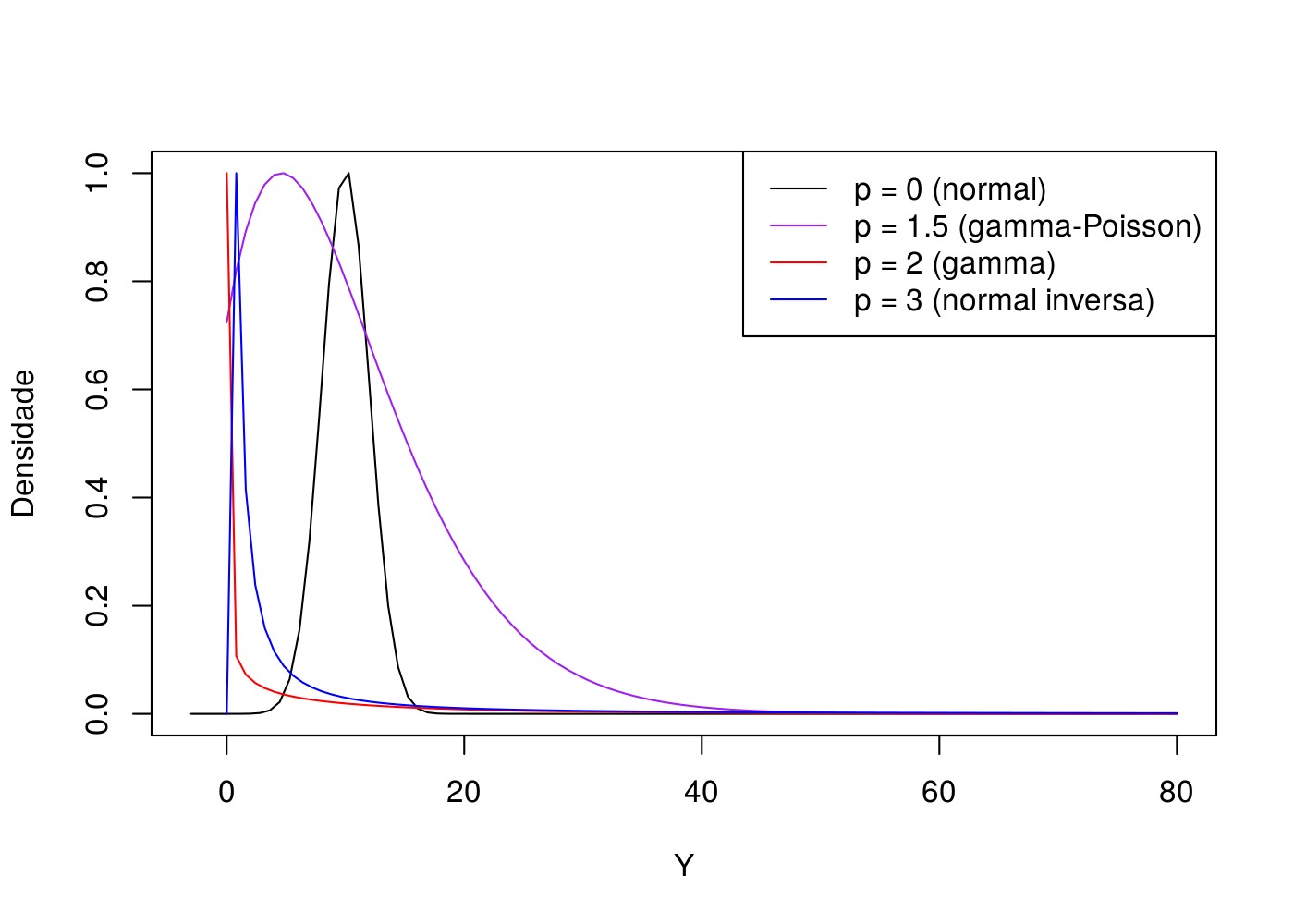
# dtweedie(0, power = 1.5, mu = 2, phi = 5)Uma vez que a distribuição normal é simétrica, a sua densidade está em torno da média, conforme esperado. A gamma-Poisson por sua vez chega a possuir um valor de densidade para Y = 0 (enquanto as outras não) e possui caráter assimétrico possuindo maior massa para valores ao redor de 5. A distribuição gamma tem maior valor de densidade para valores pequenos (até Y = 5 aproximadamente) e uma cauda pesada para os demais valores. Já a normal inversa assume maiores valores de densidade até Y = 10 em relação a distribuição gamma e cauda pesada para os demais valores de Y. Essa cauda é mais pesada que a da distribuição gamma, para isso, é necessário limitar os limites do eixo Y (isto é, dar um “zoom” no gráfico):
plot(a, type = "l", ylab = "Densidade", xlab = "Y", ylim = c(0, 0.1))
legend("topright",
col = c("black", "purple", "red", "blue"),
legend = c("p = 0 (normal)", "p = 1.5 (gamma-Poisson)","p = 2 (gamma)", "p = 3 (normal inversa)"),
lty = 1)
lines(b, col = "purple")
lines(c, col = "red")
lines(d, col = "blue")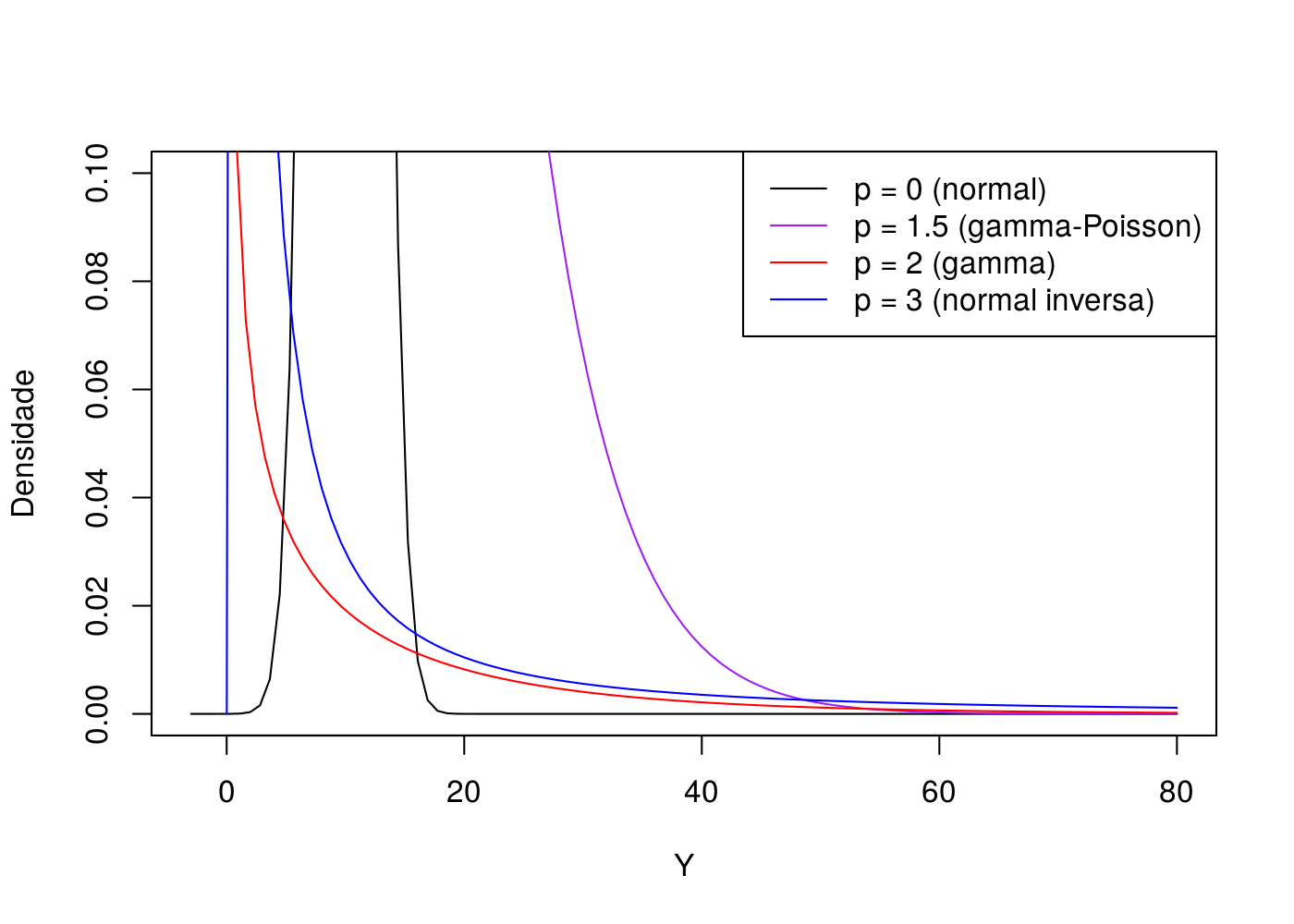
Aplicações da distribuição Tweedie em modelos de regressão
Estimação via Máxima Verossimilhança
Até aqui, foi apresentada a distribuição Tweedie a partir das suas propriedades e seus domínios, que são necessários para compreender como ela funciona na prática. Ao ajustar um modelo de regressão Tweedie no contexto de GLM, o primeiro passo é estimar o valor de \(p\), isto é, é necessário identificar qual forma da distribuição. Uma forma de se fazer isso é via máxima verossimilhança, e esse será o primeiro método abordado. Para isso, utilizaremos a função tweedie::tweedie.profile para traçar o perfil da verossimilhança para diferentes valores de \(p\) (parâmetro potência) e escolher o valor de \(p\) que maximize a função de log verossimilhança (\(l(x)\)). Em seguida, após identificarmos o valor de p que maximiza a função de log verossimilhança, iremos ajustar um GLM tweedie utilizando a família Tweedie, disponível no pacote statmod.
Para isso, foram simuladas 1000 amostras de \(Y \sim G(\alpha = 1, \beta = \frac{1}{0.5})\) sendo o primeiro o parâmetro de forma (\(\alpha = shape\)) e o segundo o parâmetro de taxa (\(\beta = rate = \frac{1}{escala }\)), cuja representação da distribuição gamma foi dada da seguinte forma: \[f(y) = \frac{\beta^{\alpha}y^{a-1}e^{-\beta y}}{\Gamma(\alpha)}\] e têm-se as seguintes propriedades:
\(E[Y] = \frac{\alpha}{\beta}\) \(V[Y] = \frac{\alpha}{\beta^2}\)
Nesse caso:
set.seed(323)
y <- rgamma(1000, shape = 1, rate = 1/0.5)
mean(y)[1] 0.53276var(y)[1] 0.26624ou seja:
\[E[Y] = \frac{\alpha}{\beta} = \frac{1}{1/0.5} = 0.5 = \widehat{\bar{Y}} = 0.53\] \[V[Y] = \frac{\alpha}{\beta^2} = \frac{1}{(1/0.5)^2} = \frac{1}{4} = 0.25 = \widehat{\sigma}^2_{Y} = 0.27\]
valores simulados muito próximos dos valores dos parâmetros.
Uma vez que os dados foram simulados, é necessário estimar o parâmetro de pontência (\(p\)), que deve ser próximo de 2, uma vez que p = 2 representa a distribuição gamma. Para realizar a estimação de p, é necessário fornecer os seguintes parâmetros:
form= nesse caso é a fórmula da regressão. Como não temos nenhuma covariável nesse exemplo, apresentaremos apenas \(y \sim 1\), caso contrário deveríamos informar as covariáveis.p.vec= um vetor de possíveis valores para o \(p\), nesse caso, será fornecido o valor 0 (que representa uma distribuição Normal), e uma sequência de 20 valores equidistantes entre o valor 1.1 e 5 (para melhor estudar o grau de assimetria dos dados;link.power= será passado o valor 0, que representa o linklog;do.plot= será passado o valorT, indicado a função para plotar o perfil de verossimilhança;do.smooth= será passado o valorF, pois não quero uma curva suave nos dados nesse primeiro momento.
Segue o gráfico da estimação de \(p\):
adj1 <- tweedie::tweedie.profile(y ~ 1,
p.vec = c(0, seq(1.1, 3, length.out = 15)),
link.power = 0,
do.plot = T,
do.smooth = F,
method = "series")0 1.1 1.2357 1.3714 1.5071 1.6429 1.7786 1.9143 2.05 2.1857 2.3214 2.4571 2.5929 2.7286 2.8643 3
................Done.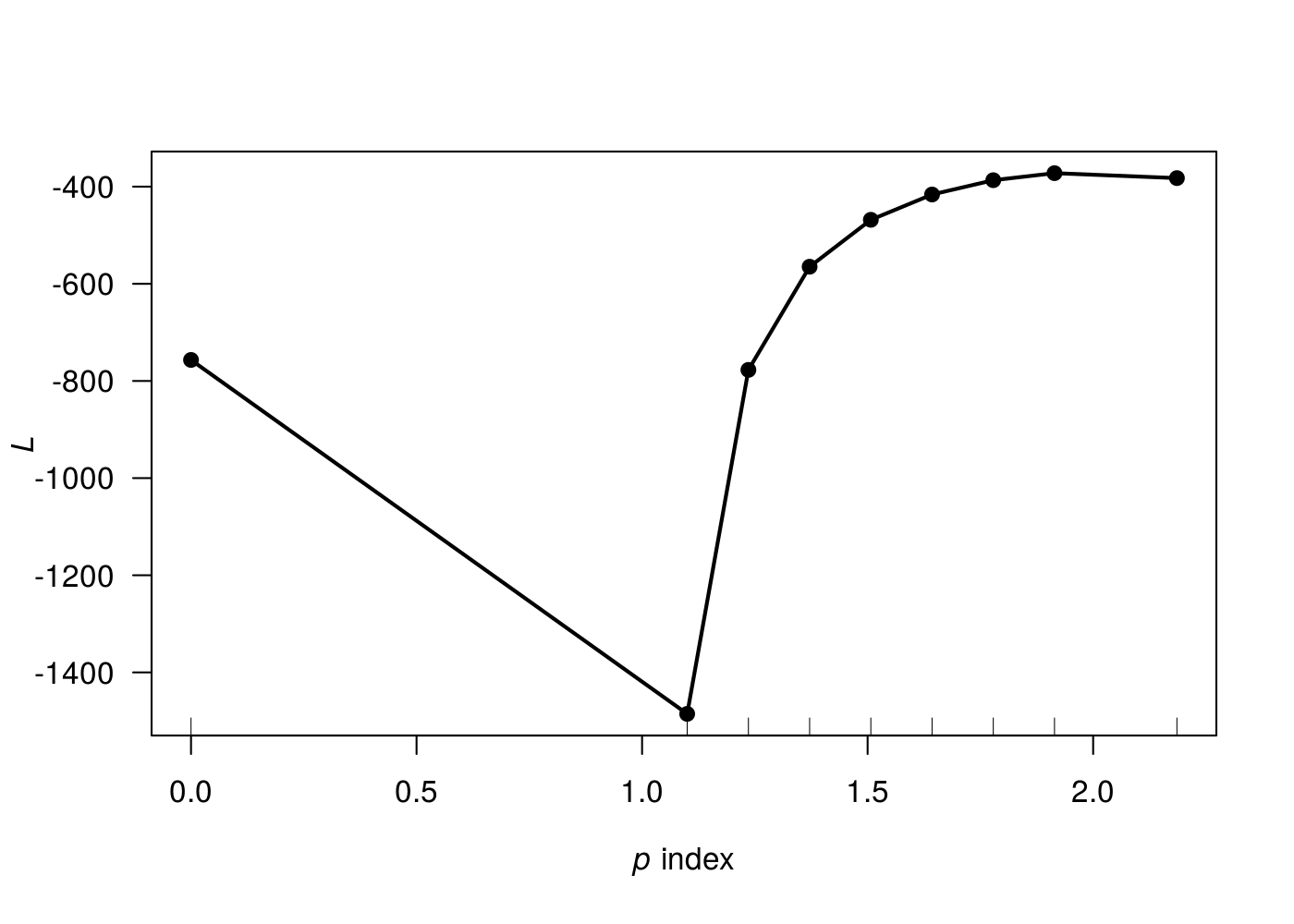
Note que para \(p=0\) temos um valor bem baixo de \(l(p)\), o que já era de se esperar, uma vez que os dados foram gerados de uma distribuição gamma. A partir do perfil da verossimilhança, nota-se que o valor de p que maximiza \(l(p)\) encontra-se próximo de 2. Ainda, o método não convergiu para valores de p superiores de 3, e ainda retornou avisos (warnings messages). Por um primeiro momento, tal aviso pode ser um pouco “intimidador”, no entanto, ao inspecionar o gráfico anterior, nota-se que não faz sentido valores de p > 3 para essa variável, e isso pode ter sido o motivo da não estimação de \(p\). A estimação do valor de \(p\) não é tão simples computacionalmente via MLE, e pode não ser estimada dependendo do valor de \(p\), e para isso, é necessário sempre checar o gráfico do perfil de \(l(p)\).
Nesse caso, faremos uma nova simulação da seguinte forma:
- Valores de \(p\) mais próximos de 2;
- Método de estimação
seriespara que a estimação de p seja mais rápida; - Solicitando o intervalo de confiança (para isso, é necessário solicitar uma curva smooth). Argumentos
do.smooth = Tedo.ci = T.
Segue resultado:
adj1 <- tweedie::tweedie.profile(y ~ 1,
p.vec = seq(1.5, 2.5, length.out = 10),
link.power = 0,
do.plot = T,
do.smooth = T,
do.ci = T,
method = "series")1.5 1.6111 1.7222 1.8333 1.9444 2.0556 2.1667 2.2778 2.3889 2.5
..........Done.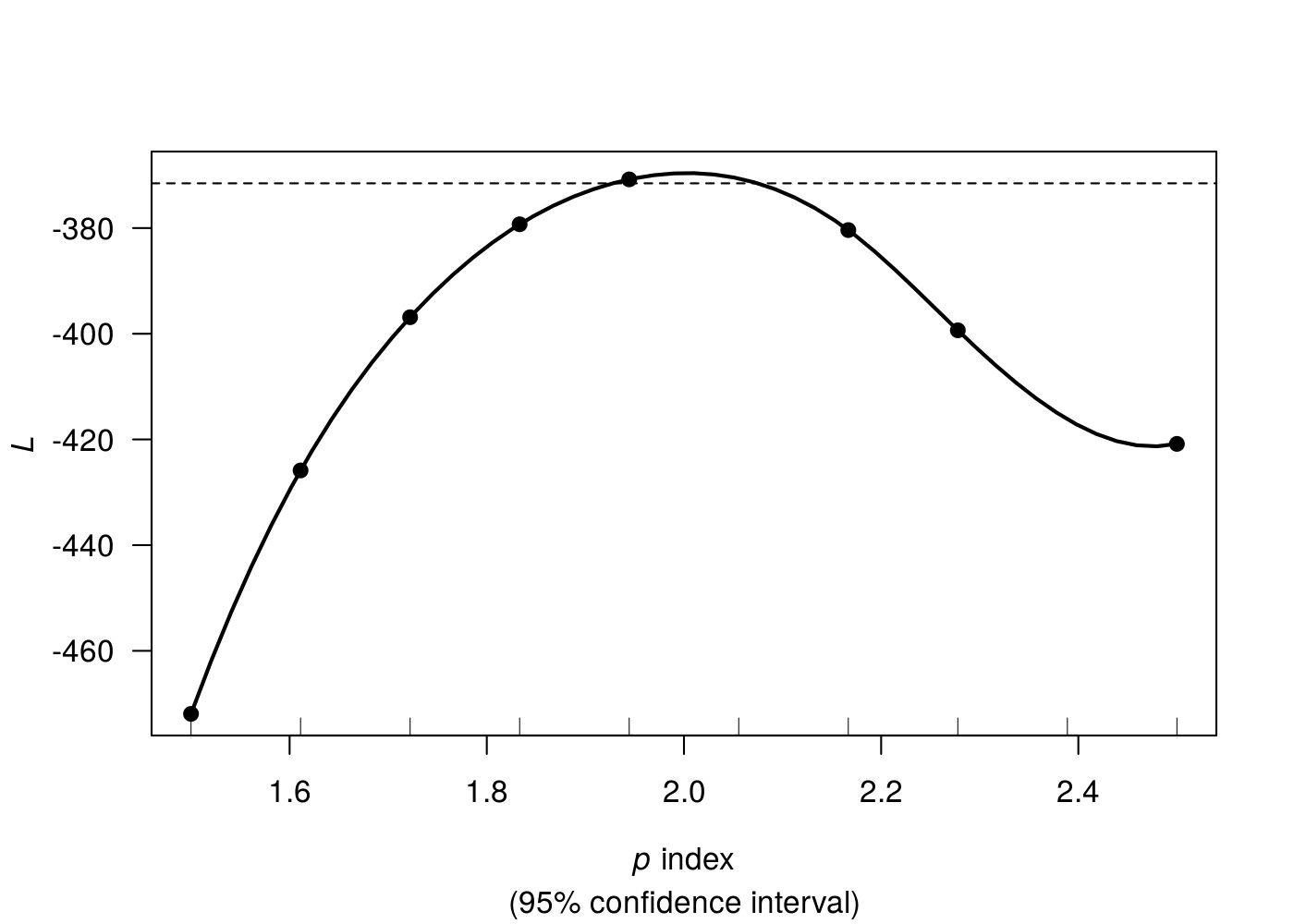
A linha horizontal pontilhada nesse caso apresenta o intervalo de confiança de 95% para o valor de \(p\). Os pontos do gráficos foram os valores de p utilizados, e a linha que conecta os pontos foi feita a partir da suavização da curva via splines.
O valor de p e do intervalo são encontrados respectivamente por:
# Estimativa pontual de p
adj1$p.max[1] 2.0102# Intervalo de confiança de p
adj1$ci[1] 1.9281 2.0787Embora o valor p = 2.010204 não tenha sido utilizado para estimar o valor de \(l(p)\), a partir da suavização foi o valor que maximiza \(l(p)\), e o mesmo será utilizado para estimar os parâmetros de regressão.
A estimação de um glm através da distribuição Tweedie é simples. Basta no argumento family especificar a função de ligação e o valor do parâmetro de potência:
m1 <- glm(y ~ 1, family = statmod::tweedie(var.power = adj1$p.max, link.power = 0))
summary(m1)
Call:
glm(formula = y ~ 1, family = statmod::tweedie(var.power = adj1$p.max,
link.power = 0))
Deviance Residuals:
Min 1Q Median 3Q Max
-3.743 -1.036 -0.315 0.333 2.798
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -0.6297 0.0306 -20.6 <2e-16 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for Tweedie family taken to be 0.94407)
Null deviance: 1116.3 on 999 degrees of freedom
Residual deviance: 1116.3 on 999 degrees of freedom
AIC: NA
Number of Fisher Scoring iterations: 6par(mfrow = c(1,3))
plot(m1, which = c(1:3))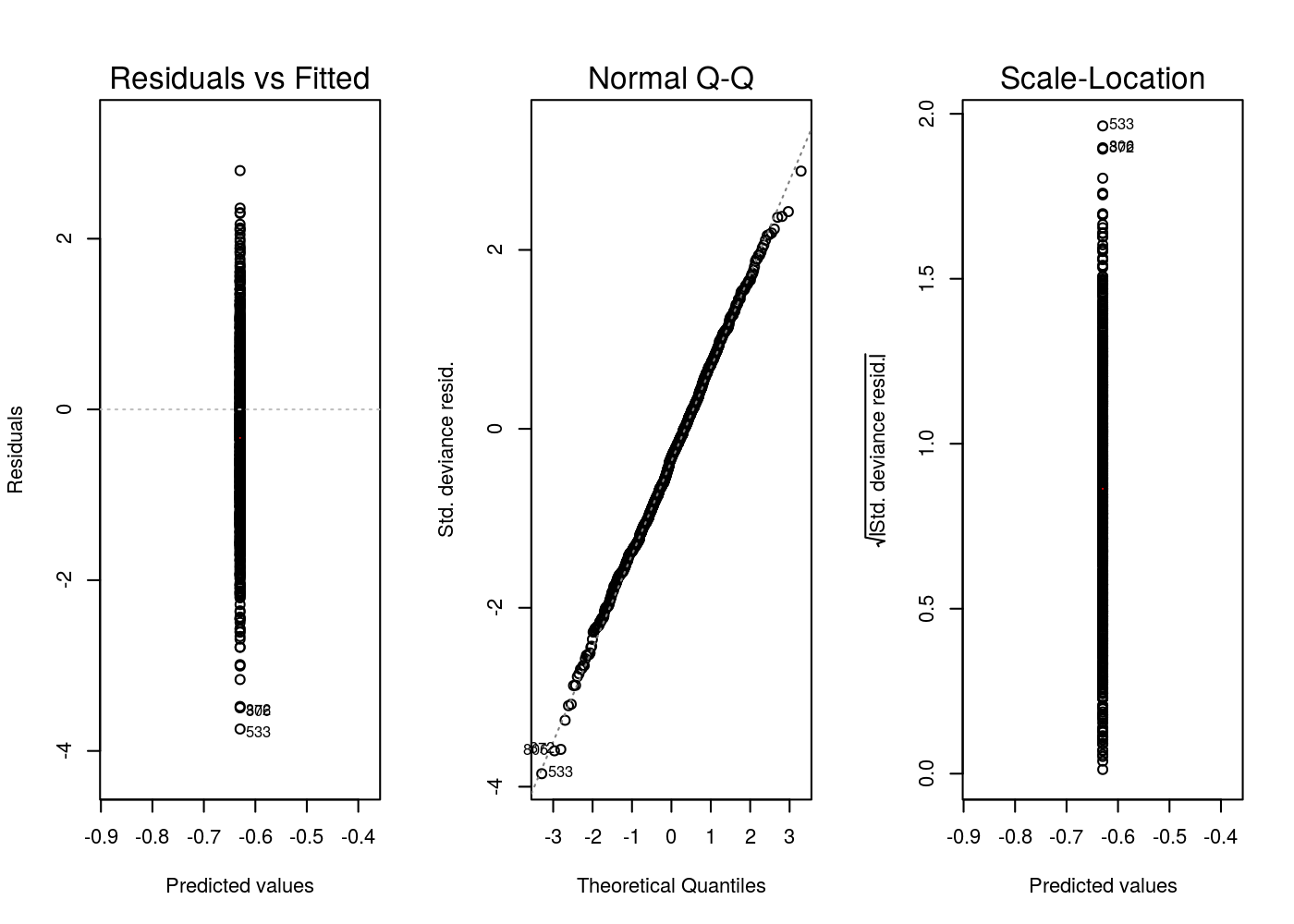
É lógico que nesse modelo o ajuste seria feito sem mais complicações. A única “desvantagem” de usar essa metodologia, é que nem todos os demais pacotes do R tem funções implementadas para a família de distribuição Tweedie. Por exemplo, fazer half-normal plots não é possível. No entanto, como o valor de p foi praticamente da distribuição Gamma, basta ajustar um modelo gamma e realizar demais verificações do modelo:
m1 <- glm(y ~ 1, family = Gamma(link = "log"))
par(mfrow = c(1,1))
hnp::hnp(m1)Gamma model 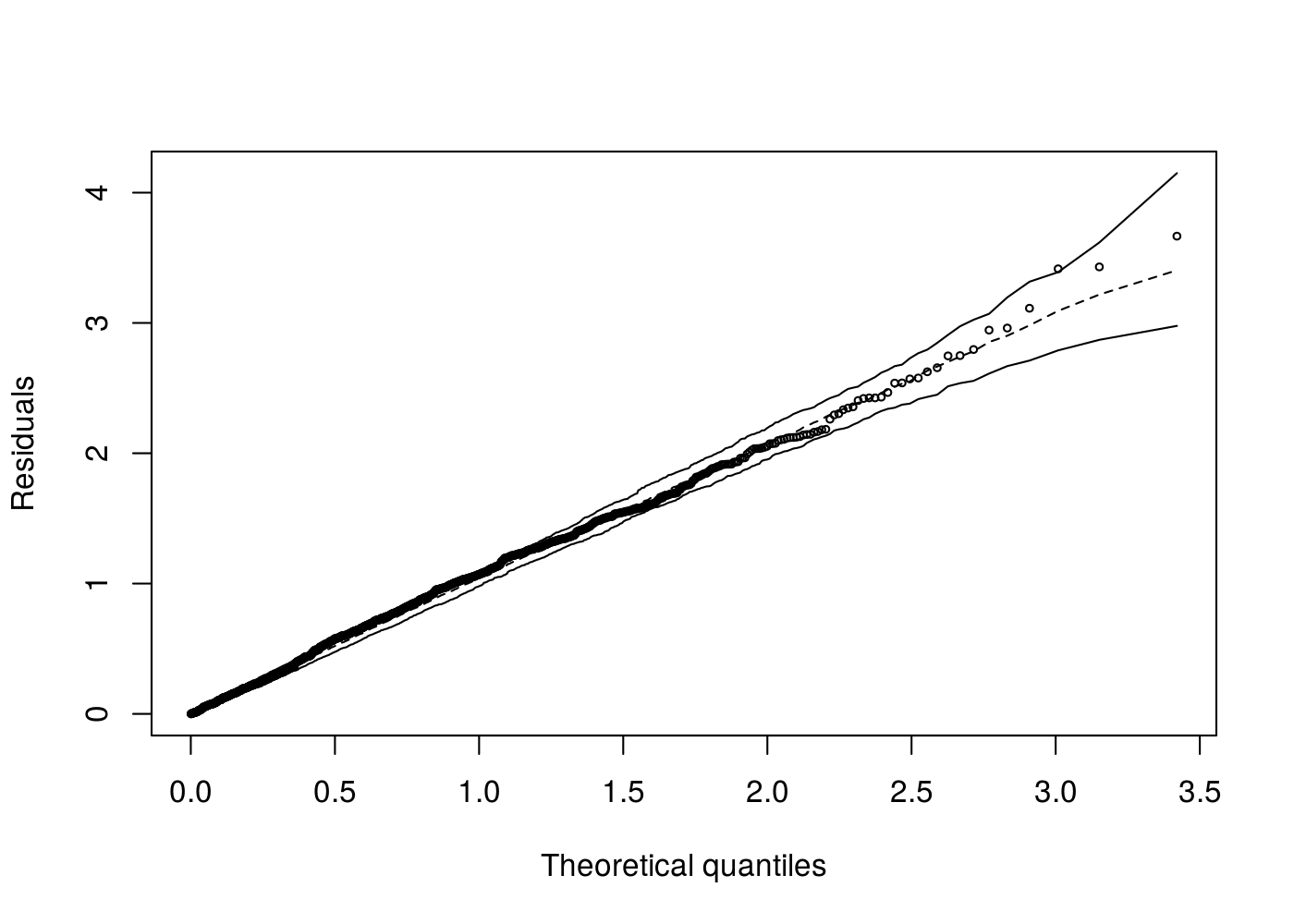
Possíveis problemas com a estimação de \(p\)
Além do problema já citado anteriormente na estimação de \(p\), existem dois outros problemas bem característicos:
- Estimação de \(p\) quando os dados seguem uma distribuição Normal
- Estimação na borda do espaço paramétrico;
iniciaremos pelo primeiro tópico.
Estimação de \(p\) quando os dados seguem uma distribuição Normal
Em conjunto de dados reais, não é possível saber de antemão qual é a distribuição da variável resposta que queremos modelar. No entanto, iremos mostrar o que acontece quando têm-se o interesse de estimar o \(\hat{p}\) de uma variável aleatória que segue uma distribuição Normal. Apresenta-se o resultado da estimação:
y.norm <- rnorm(100, mean = 20)
adj2 <- tweedie::tweedie.profile(y.norm ~ 1,
p.vec = c(0, seq(1.1, 5, length.out = 30)),
link.power = 0,
do.plot = T,
do.smooth = T,
do.ci = T,
method = "series")0 1.1 1.2345 1.369 1.5034 1.6379 1.7724 1.9069 2.0414 2.1759 2.3103 2.4448 2.5793 2.7138 2.8483 2.9828 3.1172 3.2517 3.3862 3.5207 3.6552 3.7897 3.9241 4.0586 4.1931 4.3276 4.4621 4.5966 4.731 4.8655 5
...............................Done.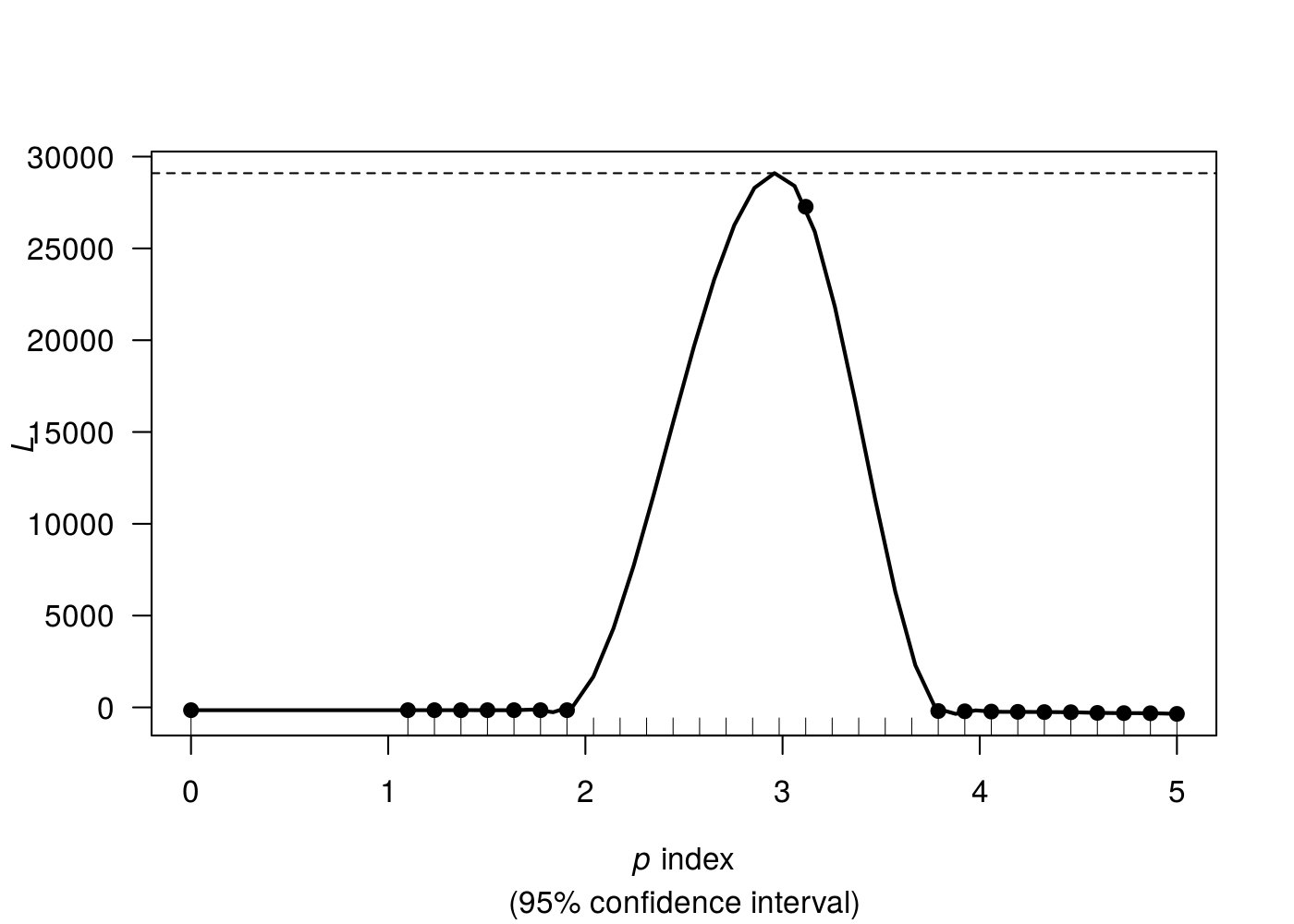
Em primeiro lugar, nota-se uma verossimilhança constante (flat) para os valores de p = 0, e entre 1 e 3 aproximadamente. Esse comportamento é típico de uma variável que segue distribuição Normal. Isso acontece, pois todas as distribuições da família Tweedie convergem para a distribuição Normal dependendo dos valores de seus parâmetros. Dessa forma, tal gráfico sugere que tanto a Normal, como a Gamma e a Normal Inversa ajustaria-se bem aos dados. Como a distribuição Normal tem melhores propriedades que as demais, escolhe-se por tal distribuição.
Outro ponto importante de salienter é que foi solicitado estimar \(l(p)\) para 30 pontos, no entanto, há um número menor deles sendo mostrados no gráfico. Isso significa que para alguns valores de p, não foi possível estimar \(l(p)\). Segue os valores de \(l(p)\) para cada p:
| l.p. | p |
|---|---|
| -151.92 | 0.0000 |
| -151.82 | 1.1000 |
| -151.81 | 1.2345 |
| -151.80 | 1.3690 |
| -151.79 | 1.5034 |
| -151.78 | 1.6379 |
| -151.78 | 1.7724 |
| -151.77 | 1.9069 |
| NaN | 2.0414 |
| NaN | 2.1759 |
| NaN | 2.3103 |
| NaN | 2.4448 |
| NaN | 2.5793 |
| -Inf | 2.7138 |
| -Inf | 2.8483 |
| -Inf | 2.9828 |
| 27269.38 | 3.1172 |
| -Inf | 3.2517 |
| -Inf | 3.3862 |
| -Inf | 3.5207 |
| -Inf | 3.6552 |
| -198.20 | 3.7897 |
| -213.24 | 3.9241 |
| -228.27 | 4.0586 |
| -243.15 | 4.1931 |
| -255.62 | 4.3276 |
| -263.17 | 4.4621 |
| -299.75 | 4.5965 |
| -311.85 | 4.7310 |
| -319.01 | 4.8655 |
| -353.61 | 5.0000 |
Nesse exemplo fica claro que é importante inspecionar o gráfico função de log verossimilhança antes de utilizar o valor de p que maximiza tal função.
Estimação de \(p\) na borda do espaço paramétrico
Aqui, queremos estimar o parâmetro \(p\) da Tweedie que foram gerados a partir de p = 1.05. Ou seja, é um conjunto de dados que contém 0 e é assimétrico. A média foi fixada em 4 e parâmetro de dispersão igual a 1. O gráfico da função de \(l(p)\) em termos de \(p\) é apresentado:
# Pacote CPLM
y.tw <- tweedie::rtweedie(100, power = 1.05, phi = 1, mu = 4)
# plot(density(y.tw))
adj2 <- tweedie::tweedie.profile(y.tw ~ 1,
p.vec = c(0, seq(1.01, 2, length.out = 20)),
link.power = 0,
do.plot = T,
do.smooth = T,
do.ci = T,
method = "series")When the response variable contains exact zeros, all values of p must be between 1 and 2; other values have been removed.
1.01 1.0621 1.1142 1.1663 1.2184 1.2705 1.3226 1.3747 1.4268 1.4789 1.5311 1.5832 1.6353 1.6874 1.7395 1.7916 1.8437 1.8958 1.9479
...................Done.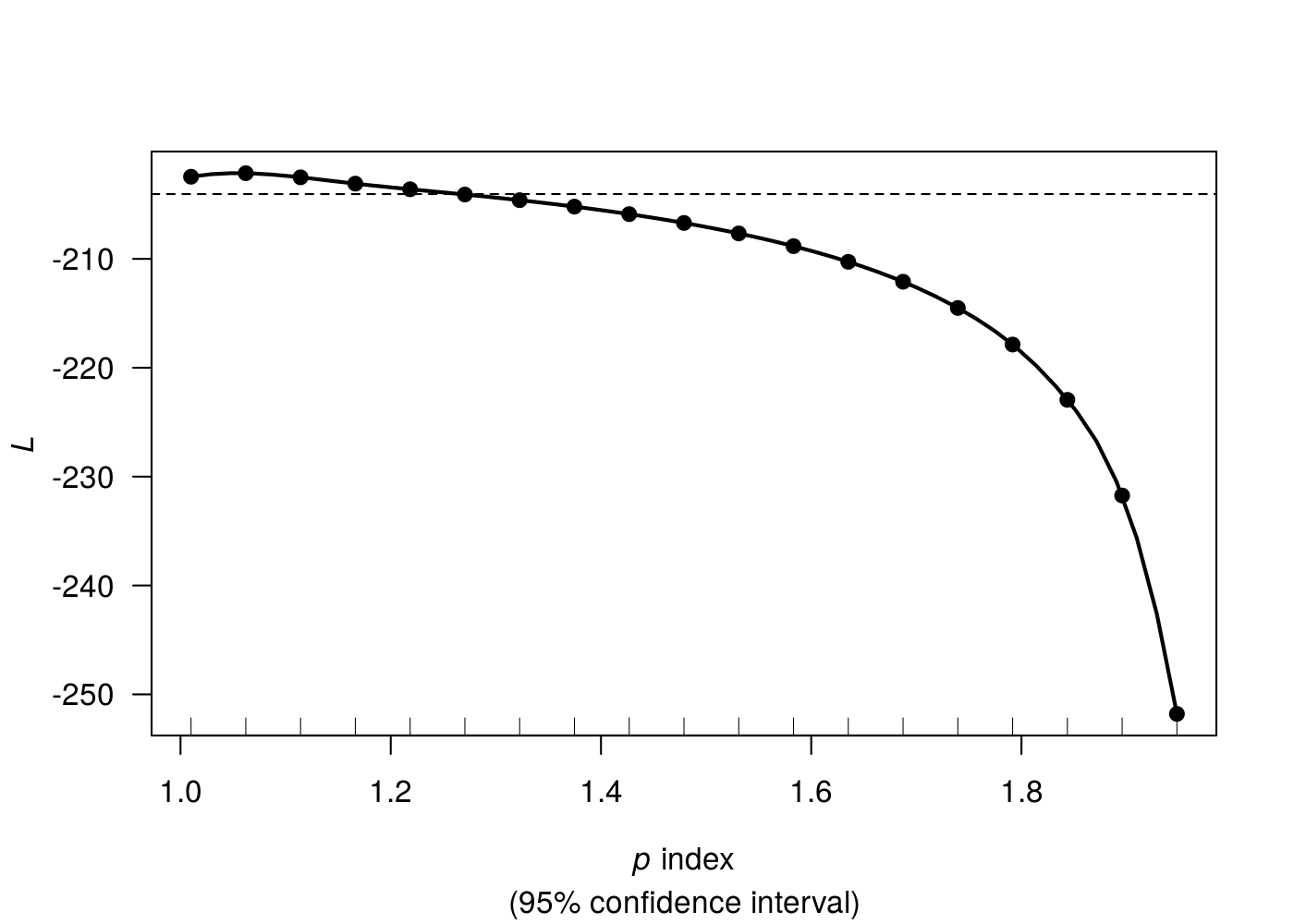
É importante ressaltar que ao tentar modelar uma variável resposta que contém 0, e estabelecer o vetor de valores p = 0, 1, …, 5 só será possível estimar p para valores entre 1 e 2. Dessa forma a própria função tweedie::tweedie.profile limita o espaço paramétrico para tais valores e noticia isso a partir da mensagem: When the response variable contains exact zeros, all values of p must be between 1 and 2; other values have been removed.
Ao usar a opção do.smooth = T a suavização estima o intervalo de confiança para o valor \(p\), e ao utilizar do.smooth = F não é possível calcular um IC.
Quando tenta-se estimar o valor de \(p\) na borda do espaço paramétrico, uma mensagem de erro comum é unable to estimate left CI que não apareceu aqui, mas em problemas com mais variáveis e dados reais é bem provável que aconteça. Tal mensagem quer dizer: não é possível avaliar \(l(p)\) para valores p a esquerda do ponto de máximo. Uma alternativa é aumentar o número de valores de \(p\) à esquerda, desde que sejam próximos do valor de \(p\) que maximiza \(l(p)\).
Estimação via quase-verossimilhança
A estimação do parâmetro de potência \(p\) agora será tratado num contexto de quase-verossimilhança. Aqui, não é necessário traçar o perfil da verossimilhança (ou da pseudo-verossimilhança no caso) em uma primeira etapa, para então fornecer o valor de \(p\) para o ajuste. Para isso, irei utilizar a função mcglm::mcglm que estima o valor de \(p\) automaticamente no processo de estimação dos parâmetros do modelo (BONAT, 2016). A grande versatilidade do pacote é que permite ajustar um modelo multivarido (múltiplas respostas) com diferentes estruturas de média (generalizado) para dados correlacionados (dados longitudinais/temporais/espaciais/medidas repetidas) (BONAT; JØRGENSEN, 2016). A única diferença, é que é necessário incluir uma covariável correlacionada com a variável resposta para estimar o parâmetro de potência, pois não sabe-se a forma da densidade, como no caso da estimação via verossimilhança.
Sendo assim, foi gerado a variável resposta Y com distribuição Gamma condicional a média X:
\[Y\mid x \sim G(\mu(x), \phi)\]
E a média foi gerada a partir de uma equação de regressão, isto é:
\[ln(\mu) = \beta_{0} + \beta_{1}x\]
em que X:
\[X\sim U (0, 1)\]
Segue o gráfico de dispersão entre as variáveis Y e X:
set.seed(323)
x <- runif(200)
b0 <- 2;b1 <- 0.5;phi <- 1.3
set.seed(888)
y <- rgamma(200, shape = exp(b0 + b1*x), rate = 1/phi)
# mean(y)
# mean(exp(b0 + b1*x))/(1/phi)
data <- data.frame(y = y,
x = x)
with(data, plot(y ~ x))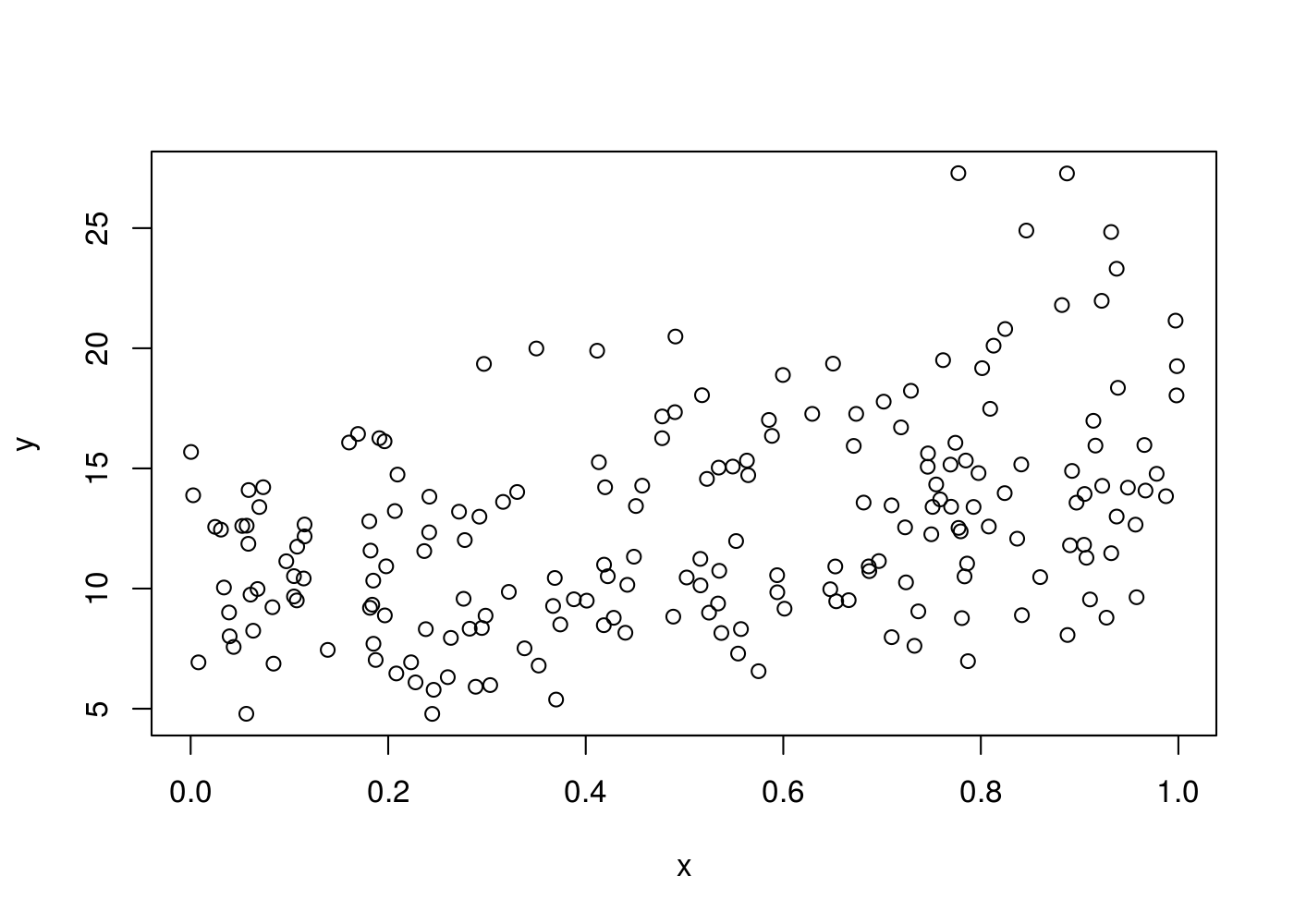
# abline(a = 2, b = 0.5, col = "blue")
# abline(coef = exp(c(2.28, 0.47)), col = "red")Nota-se uma relação positiva entre ambas variáveis (uma vez que foi induzida pelo modelo). Agora, será ajustado um modelo de regressão de Y em função de X. Para tal, iremos especificar os seguintes parâmetros:
matrix_pred: Matriz que identifica a estrutura de covariância nos dados. Nesse caso, é apenas uma matriz diagonal identidade (pois não tem estrutura de dependência dos dados).control_algorithm: Controla a estimação dos parâmetros do modelo de regressão através algoritimo.Tuning = 0.35faz com que o algoritmo seja estudada de forma mais lenta, no entanto, permite o ajuste;Max_iter = 0.5permite o algoritmo iterar mais vezes que o padrão (20);variance: Estrutura de variância para o modelo, nesse casoTweedie;power_fixed: Para o modelo estimar o parâmetro de potência daTweedie, é necessário deixar comoF;link: Função de ligação utilizada para a média, nesse caso, linklog.
Segue o summary do modelo ajustado:
z0 <- mcglm::mc_id(data)
m1 <- mcglm::mcglm(c(y ~ x),
matrix_pred = list(z0),
link = "log",
variance = "tweedie",
power_fixed = F,
data = data,
control_algorithm = list(tuning = 0.35, max_iter = 50))Automatic initial values selected. summary(m1)Call: y ~ x
Link function: log
Variance function: tweedie
Covariance function: identity
Regression:
Estimates Std.error Z value
(Intercept) 2.28347 0.042772 53.3867
x 0.46811 0.072647 6.4436
Power:
Estimates Std.error Z value
1 2.0549 0.66198 3.1041
Dispersion:
Estimates Std.error Z value
1 0.081936 0.13502 0.60682
Algorithm: chaser
Correction: TRUE
Number iterations: 22As estimativas dos parâmetros de regressão foram próximos aos induzidos pelo modelo (\(\beta_{0} = 2;\beta_{1} = 0.5\)). O parâmetro de potência foi igual a 2.05, valor esse próximo de 2. As interpretações dos parâmetros são feitos de forma análoga a da função glm utilizando family = Gamma(link = "log"). Para validar o modelo, segue análise de resíduos:
plot(m1)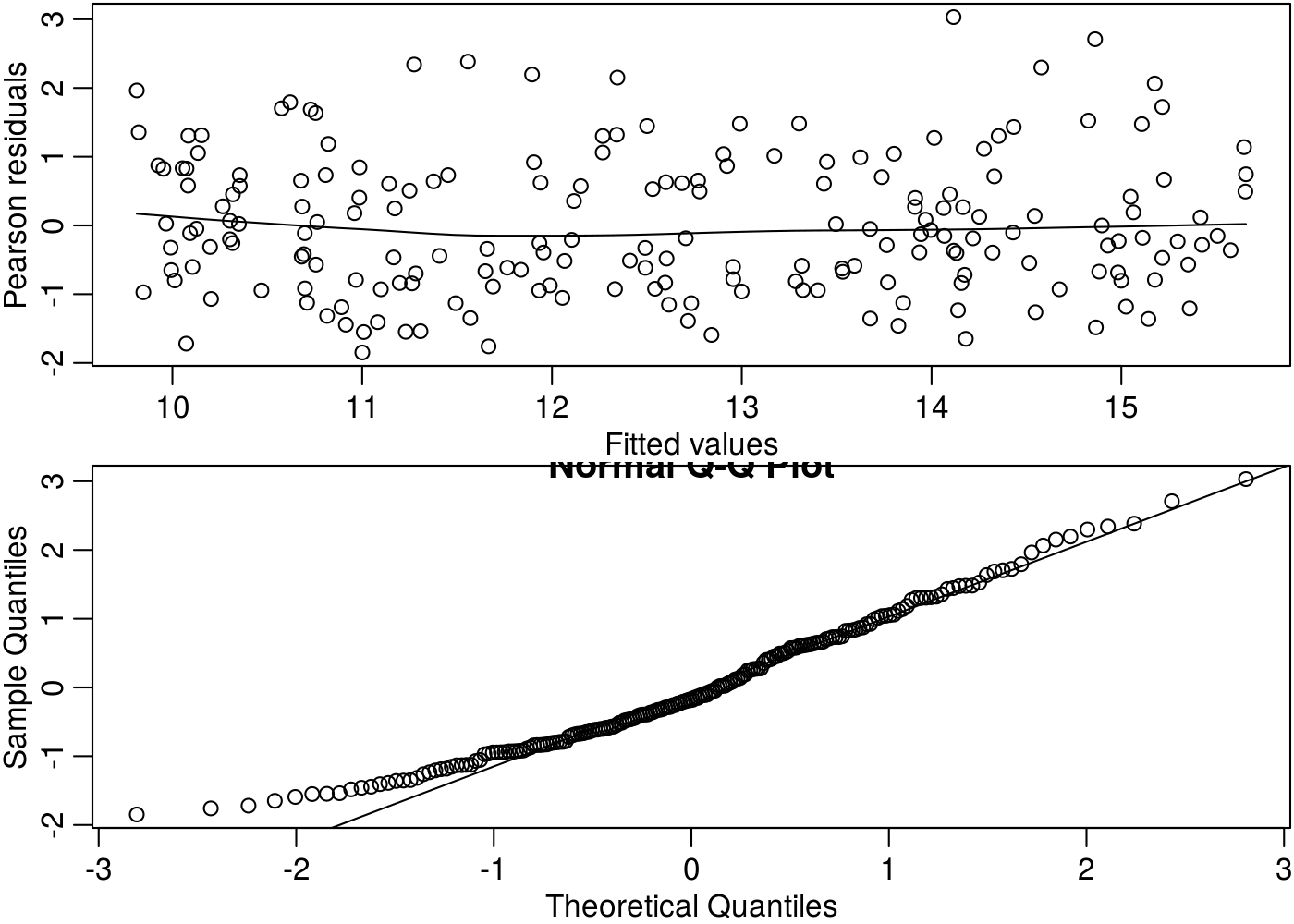
Não nota-se relação média e variância nos resíduos em relação aos valores ajustados. O fato de uma pequena fuga de normalidade nesse gráfico não é um problema, uma vez que os resíduos não seguem uma distribuição normal (uma vez que a distribuição utilizada é a gamma, assimétrica).
Aplicação da Tweedie em modelos GAM
Contexto e metodologia
Uma outra utilidade de tal distribuição é na abordagem dos modelos aditivos generalizados (GAM). Imagine que tenhamos um problema em que eu tenho uma variável resposta positiva assimétrica que contém 0 e outra variável numérica qualquer e desejo verificar se as duas estão correlacionadas. Após fazer o gráfico de dispersão, nota-se que a relação entre as duas é não linear, inviabilizando assim, o cálculo do coeficiente de correlação de Pearson, que já foi apresentado nesse post. Como alternativa, é possível estimar uma curva suave para a relação entre y e x a partir da função mgcv::gam. Ela não retorna um coeficiente de correlação em si, no entanto permite visualizar graficamente tal relação. Os modelos GAM estendem os modelos GLM no sentido de ser possível estimar uma relação não linear entre uma covariável numérica e uma preditora numérica. Essa função suave, por exemplo, pode ser estimada tanto por polinômios locais, splines e densidade de kernel. A escolha da função suave normalmente é feita internamente pelo pacote através da função s(), entretanto, nesse exemplo foi necessário calibrar alguns parâmetros.
Aplicação
O conjunto de dados utilizado nesse exemplo foi de Swedish Motor Insurance que foi publicado em FREES (2009) e podemos baixá-lo aqui, cuja documentação está diponível aqui. Basicamente, estamos interessado em modelar o total de pagamentos feita pela companhia de seguros (Payment) em relação o número de anos do segurados (insured).
Na tabela abaixo é possível visualizar o conjunto de dados, cujas colunas em azul representam as variáveis utilizadas:| Kilometres | Zone | Bonus | Make | Insured | Claims | Payment |
|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 455.13 | 108 | 392491 |
| 1 | 1 | 1 | 2 | 69.17 | 19 | 46221 |
| 1 | 1 | 1 | 3 | 72.88 | 13 | 15694 |
| 1 | 1 | 1 | 4 | 1292.39 | 124 | 422201 |
| 1 | 1 | 1 | 5 | 191.01 | 40 | 119373 |
| 1 | 1 | 1 | 6 | 477.66 | 57 | 170913 |
| 1 | 1 | 1 | 7 | 105.58 | 23 | 56940 |
| 1 | 1 | 1 | 8 | 32.55 | 14 | 77487 |
| 1 | 1 | 1 | 9 | 9998.46 | 1704 | 6805992 |
| 1 | 1 | 2 | 1 | 314.58 | 45 | 214011 |
| 1 | 1 | 2 | 2 | 61.82 | 10 | 65303 |
| 1 | 1 | 2 | 3 | 47.06 | 5 | 20871 |
| 1 | 1 | 2 | 4 | 782.58 | 48 | 242894 |
| 1 | 1 | 2 | 5 | 115.43 | 11 | 23545 |
| 1 | 1 | 2 | 6 | 338.06 | 23 | 39598 |
| 1 | 1 | 2 | 7 | 70.44 | 7 | 48767 |
| 1 | 1 | 2 | 8 | 15.25 | 2 | 6560 |
| 1 | 1 | 2 | 9 | 6416.19 | 638 | 2873487 |
| 1 | 1 | 3 | 1 | 309.98 | 24 | 134931 |
| 1 | 1 | 3 | 2 | 49.18 | 6 | 50908 |
| 1 | 1 | 3 | 3 | 32.02 | 3 | 4399 |
| 1 | 1 | 3 | 4 | 497.20 | 23 | 112992 |
| 1 | 1 | 3 | 5 | 73.48 | 6 | 14788 |
| 1 | 1 | 3 | 6 | 278.01 | 9 | 48713 |
| 1 | 1 | 3 | 7 | 66.36 | 9 | 52076 |
| 1 | 1 | 3 | 8 | 17.86 | 3 | 13161 |
| 1 | 1 | 3 | 9 | 5063.15 | 408 | 1707680 |
| 1 | 1 | 4 | 1 | 318.48 | 29 | 103866 |
| 1 | 1 | 4 | 2 | 57.21 | 7 | 77588 |
| 1 | 1 | 4 | 3 | 35.33 | 4 | 11839 |
| 1 | 1 | 4 | 4 | 374.28 | 20 | 98140 |
| 1 | 1 | 4 | 5 | 85.18 | 7 | 27919 |
| 1 | 1 | 4 | 6 | 199.70 | 7 | 103910 |
| 1 | 1 | 4 | 7 | 60.46 | 4 | 38065 |
| 1 | 1 | 4 | 8 | 12.74 | 0 | 0 |
| 1 | 1 | 4 | 9 | 4263.09 | 300 | 1267678 |
| 1 | 1 | 5 | 1 | 444.37 | 25 | 69203 |
| 1 | 1 | 5 | 2 | 86.65 | 6 | 14620 |
| 1 | 1 | 5 | 3 | 53.81 | 5 | 40258 |
| 1 | 1 | 5 | 4 | 361.62 | 22 | 161455 |
| 1 | 1 | 5 | 5 | 117.91 | 3 | 20011 |
| 1 | 1 | 5 | 6 | 232.55 | 11 | 57214 |
| 1 | 1 | 5 | 7 | 81.27 | 3 | 4496 |
| 1 | 1 | 5 | 8 | 18.21 | 0 | 0 |
| 1 | 1 | 5 | 9 | 4761.37 | 301 | 1116208 |
| 1 | 1 | 6 | 1 | 1016.67 | 61 | 217617 |
| 1 | 1 | 6 | 2 | 150.56 | 12 | 58099 |
| 1 | 1 | 6 | 3 | 126.69 | 4 | 12268 |
| 1 | 1 | 6 | 4 | 517.31 | 16 | 59634 |
| 1 | 1 | 6 | 5 | 246.62 | 13 | 84966 |
| 1 | 1 | 6 | 6 | 482.96 | 19 | 137005 |
| 1 | 1 | 6 | 7 | 203.60 | 12 | 33767 |
| 1 | 1 | 6 | 8 | 25.88 | 3 | 6279 |
| 1 | 1 | 6 | 9 | 9197.99 | 522 | 1939894 |
| 1 | 1 | 7 | 1 | 5430.48 | 214 | 1048698 |
| 1 | 1 | 7 | 2 | 659.54 | 24 | 143915 |
| 1 | 1 | 7 | 3 | 657.34 | 22 | 153830 |
| 1 | 1 | 7 | 4 | 2795.72 | 60 | 202413 |
| 1 | 1 | 7 | 5 | 1119.12 | 41 | 180345 |
| 1 | 1 | 7 | 6 | 2861.69 | 92 | 484604 |
| 1 | 1 | 7 | 7 | 1111.00 | 37 | 152801 |
| 1 | 1 | 7 | 8 | 166.61 | 6 | 14084 |
| 1 | 1 | 7 | 9 | 48264.64 | 1875 | 8977527 |
| 1 | 2 | 1 | 1 | 458.89 | 98 | 532092 |
| 1 | 2 | 1 | 2 | 72.78 | 5 | 9006 |
| 1 | 2 | 1 | 3 | 33.23 | 7 | 45498 |
| 1 | 2 | 1 | 4 | 1544.55 | 101 | 337480 |
| 1 | 2 | 1 | 5 | 200.90 | 43 | 191982 |
| 1 | 2 | 1 | 6 | 663.98 | 65 | 300632 |
| 1 | 2 | 1 | 7 | 124.73 | 10 | 23349 |
| 1 | 2 | 1 | 8 | 29.24 | 4 | 13581 |
| 1 | 2 | 1 | 9 | 11381.00 | 1326 | 6173598 |
| 1 | 2 | 2 | 1 | 364.78 | 40 | 211494 |
| 1 | 2 | 2 | 2 | 51.89 | 5 | 10811 |
| 1 | 2 | 2 | 3 | 29.39 | 4 | 36204 |
| 1 | 2 | 2 | 4 | 1053.01 | 33 | 135007 |
| 1 | 2 | 2 | 5 | 110.10 | 16 | 49061 |
| 1 | 2 | 2 | 6 | 470.62 | 30 | 64287 |
| 1 | 2 | 2 | 7 | 93.29 | 8 | 51080 |
| 1 | 2 | 2 | 8 | 17.88 | 1 | 600 |
| 1 | 2 | 2 | 9 | 7607.66 | 591 | 2510207 |
| 1 | 2 | 3 | 1 | 315.14 | 17 | 106975 |
| 1 | 2 | 3 | 2 | 64.53 | 4 | 16922 |
| 1 | 2 | 3 | 3 | 27.24 | 2 | 8255 |
| 1 | 2 | 3 | 4 | 726.13 | 29 | 93656 |
| 1 | 2 | 3 | 5 | 96.49 | 4 | 44966 |
| 1 | 2 | 3 | 6 | 365.81 | 16 | 43426 |
| 1 | 2 | 3 | 7 | 80.80 | 5 | 48691 |
| 1 | 2 | 3 | 8 | 13.30 | 1 | 1325 |
| 1 | 2 | 3 | 9 | 5898.98 | 320 | 1392652 |
| 1 | 2 | 4 | 1 | 320.47 | 16 | 136143 |
| 1 | 2 | 4 | 2 | 69.55 | 4 | 34137 |
| 1 | 2 | 4 | 3 | 33.37 | 1 | 2702 |
| 1 | 2 | 4 | 4 | 507.57 | 9 | 22292 |
| 1 | 2 | 4 | 5 | 72.40 | 7 | 20295 |
| 1 | 2 | 4 | 6 | 316.14 | 9 | 57404 |
| 1 | 2 | 4 | 7 | 72.05 | 3 | 8538 |
| 1 | 2 | 4 | 8 | 18.35 | 0 | 0 |
| 1 | 2 | 4 | 9 | 4957.56 | 269 | 1375988 |
| 1 | 2 | 5 | 1 | 473.63 | 27 | 136376 |
| 1 | 2 | 5 | 2 | 88.09 | 8 | 19038 |
| 1 | 2 | 5 | 3 | 46.27 | 2 | 3604 |
| 1 | 2 | 5 | 4 | 467.96 | 9 | 10597 |
| 1 | 2 | 5 | 5 | 126.88 | 10 | 26433 |
| 1 | 2 | 5 | 6 | 316.15 | 11 | 52950 |
| 1 | 2 | 5 | 7 | 101.11 | 7 | 21620 |
| 1 | 2 | 5 | 8 | 23.37 | 1 | 2680 |
| 1 | 2 | 5 | 9 | 5481.31 | 282 | 1079230 |
| 1 | 2 | 6 | 1 | 996.27 | 61 | 236220 |
| 1 | 2 | 6 | 2 | 175.14 | 10 | 25036 |
| 1 | 2 | 6 | 3 | 111.97 | 5 | 22261 |
| 1 | 2 | 6 | 4 | 601.61 | 16 | 88961 |
| 1 | 2 | 6 | 5 | 260.69 | 14 | 64368 |
| 1 | 2 | 6 | 6 | 593.18 | 17 | 65578 |
| 1 | 2 | 6 | 7 | 229.72 | 7 | 46244 |
| 1 | 2 | 6 | 8 | 46.66 | 7 | 14385 |
| 1 | 2 | 6 | 9 | 9830.72 | 413 | 1840742 |
| 1 | 2 | 7 | 1 | 6021.43 | 233 | 1086534 |
| 1 | 2 | 7 | 2 | 852.80 | 33 | 165960 |
| 1 | 2 | 7 | 3 | 751.59 | 24 | 100564 |
| 1 | 2 | 7 | 4 | 3293.99 | 60 | 201401 |
| 1 | 2 | 7 | 5 | 1289.09 | 53 | 272610 |
| 1 | 2 | 7 | 6 | 3665.27 | 97 | 524316 |
| 1 | 2 | 7 | 7 | 1369.91 | 35 | 159658 |
| 1 | 2 | 7 | 8 | 183.98 | 5 | 18603 |
| 1 | 2 | 7 | 9 | 55084.54 | 1744 | 8500391 |
| 1 | 3 | 1 | 1 | 453.06 | 72 | 329632 |
| 1 | 3 | 1 | 2 | 67.13 | 9 | 79565 |
| 1 | 3 | 1 | 3 | 35.22 | 5 | 11746 |
| 1 | 3 | 1 | 4 | 1653.17 | 89 | 338305 |
| 1 | 3 | 1 | 5 | 206.62 | 38 | 124108 |
| 1 | 3 | 1 | 6 | 859.95 | 64 | 213078 |
| 1 | 3 | 1 | 7 | 110.08 | 11 | 34844 |
| 1 | 3 | 1 | 8 | 25.92 | 5 | 25319 |
| 1 | 3 | 1 | 9 | 11436.08 | 1205 | 5173923 |
| 1 | 3 | 2 | 1 | 317.10 | 25 | 90162 |
| 1 | 3 | 2 | 2 | 54.58 | 8 | 19327 |
| 1 | 3 | 2 | 3 | 22.59 | 3 | 1209 |
| 1 | 3 | 2 | 4 | 1187.43 | 30 | 123124 |
| 1 | 3 | 2 | 5 | 129.53 | 13 | 99258 |
| 1 | 3 | 2 | 6 | 617.11 | 40 | 137828 |
| 1 | 3 | 2 | 7 | 102.50 | 7 | 14904 |
| 1 | 3 | 2 | 8 | 21.56 | 1 | 597 |
| 1 | 3 | 2 | 9 | 8351.79 | 425 | 1937445 |
| 1 | 3 | 3 | 1 | 357.43 | 18 | 37835 |
| 1 | 3 | 3 | 2 | 62.87 | 3 | 5014 |
| 1 | 3 | 3 | 3 | 18.00 | 0 | 0 |
| 1 | 3 | 3 | 4 | 849.23 | 25 | 61591 |
| 1 | 3 | 3 | 5 | 119.21 | 6 | 47495 |
| 1 | 3 | 3 | 6 | 463.60 | 20 | 53173 |
| 1 | 3 | 3 | 7 | 104.36 | 6 | 11936 |
| 1 | 3 | 3 | 8 | 14.21 | 1 | 31442 |
| 1 | 3 | 3 | 9 | 6540.44 | 304 | 1284025 |
| 1 | 3 | 4 | 1 | 338.37 | 19 | 136281 |
| 1 | 3 | 4 | 2 | 52.49 | 2 | 9253 |
| 1 | 3 | 4 | 3 | 27.97 | 0 | 0 |
| 1 | 3 | 4 | 4 | 571.94 | 23 | 142536 |
| 1 | 3 | 4 | 5 | 113.36 | 6 | 21433 |
| 1 | 3 | 4 | 6 | 406.33 | 21 | 131027 |
| 1 | 3 | 4 | 7 | 85.15 | 3 | 4079 |
| 1 | 3 | 4 | 8 | 16.16 | 1 | 1012 |
| 1 | 3 | 4 | 9 | 5123.78 | 217 | 994540 |
| 1 | 3 | 5 | 1 | 459.40 | 16 | 61958 |
| 1 | 3 | 5 | 2 | 73.51 | 2 | 5056 |
| 1 | 3 | 5 | 3 | 41.51 | 4 | 44278 |
| 1 | 3 | 5 | 4 | 517.24 | 8 | 18455 |
| 1 | 3 | 5 | 5 | 136.08 | 8 | 28248 |
| 1 | 3 | 5 | 6 | 417.71 | 11 | 15568 |
| 1 | 3 | 5 | 7 | 103.07 | 1 | 8347 |
| 1 | 3 | 5 | 8 | 26.11 | 1 | 1144 |
| 1 | 3 | 5 | 9 | 5849.14 | 242 | 1184032 |
| 1 | 3 | 6 | 1 | 1060.28 | 43 | 245621 |
| 1 | 3 | 6 | 2 | 124.82 | 7 | 12648 |
| 1 | 3 | 6 | 3 | 119.17 | 2 | 5855 |
| 1 | 3 | 6 | 4 | 639.97 | 12 | 64278 |
| 1 | 3 | 6 | 5 | 307.56 | 14 | 90310 |
| 1 | 3 | 6 | 6 | 740.33 | 24 | 117763 |
| 1 | 3 | 6 | 7 | 233.83 | 7 | 20303 |
| 1 | 3 | 6 | 8 | 53.41 | 3 | 6221 |
| 1 | 3 | 6 | 9 | 10263.04 | 393 | 2026554 |
| 1 | 3 | 7 | 1 | 7155.96 | 197 | 980780 |
| 1 | 3 | 7 | 2 | 999.32 | 32 | 168854 |
| 1 | 3 | 7 | 3 | 1049.99 | 19 | 41459 |
| 1 | 3 | 7 | 4 | 3712.23 | 67 | 229231 |
| 1 | 3 | 7 | 5 | 1862.44 | 74 | 388511 |
| 1 | 3 | 7 | 6 | 4964.00 | 121 | 622350 |
| 1 | 3 | 7 | 7 | 1785.23 | 58 | 253660 |
| 1 | 3 | 7 | 8 | 331.45 | 8 | 94395 |
| 1 | 3 | 7 | 9 | 65617.47 | 1865 | 9884008 |
| 1 | 4 | 1 | 1 | 868.60 | 115 | 627513 |
| 1 | 4 | 1 | 2 | 122.54 | 10 | 113492 |
| 1 | 4 | 1 | 3 | 55.08 | 3 | 33925 |
| 1 | 4 | 1 | 4 | 2751.70 | 98 | 578698 |
| 1 | 4 | 1 | 5 | 328.36 | 36 | 149698 |
| 1 | 4 | 1 | 6 | 1730.51 | 105 | 604161 |
| 1 | 4 | 1 | 7 | 231.91 | 13 | 55103 |
| 1 | 4 | 1 | 8 | 48.77 | 4 | 34267 |
| 1 | 4 | 1 | 9 | 20153.28 | 1446 | 6605073 |
| 1 | 4 | 2 | 1 | 622.23 | 41 | 300510 |
| 1 | 4 | 2 | 2 | 94.03 | 5 | 11936 |
| 1 | 4 | 2 | 3 | 36.73 | 2 | 6387 |
| 1 | 4 | 2 | 4 | 2037.95 | 48 | 152944 |
| 1 | 4 | 2 | 5 | 189.27 | 17 | 40047 |
| 1 | 4 | 2 | 6 | 1217.01 | 65 | 344450 |
| 1 | 4 | 2 | 7 | 155.50 | 16 | 113524 |
| 1 | 4 | 2 | 8 | 27.27 | 0 | 0 |
| 1 | 4 | 2 | 9 | 14648.20 | 645 | 3150912 |
| 1 | 4 | 3 | 1 | 613.17 | 32 | 168882 |
| 1 | 4 | 3 | 2 | 108.40 | 5 | 43676 |
| 1 | 4 | 3 | 3 | 37.20 | 0 | 0 |
| 1 | 4 | 3 | 4 | 1447.58 | 25 | 66208 |
| 1 | 4 | 3 | 5 | 168.81 | 8 | 30465 |
| 1 | 4 | 3 | 6 | 933.44 | 40 | 374818 |
| 1 | 4 | 3 | 7 | 153.11 | 5 | 38157 |
| 1 | 4 | 3 | 8 | 32.44 | 2 | 8234 |
| 1 | 4 | 3 | 9 | 11314.54 | 427 | 2035982 |
| 1 | 4 | 4 | 1 | 573.86 | 29 | 214513 |
| 1 | 4 | 4 | 2 | 103.82 | 4 | 12077 |
| 1 | 4 | 4 | 3 | 49.14 | 2 | 12947 |
| 1 | 4 | 4 | 4 | 970.81 | 20 | 77705 |
| 1 | 4 | 4 | 5 | 135.49 | 6 | 16781 |
| 1 | 4 | 4 | 6 | 740.62 | 25 | 87155 |
| 1 | 4 | 4 | 7 | 123.63 | 3 | 11469 |
| 1 | 4 | 4 | 8 | 36.98 | 1 | 2572 |
| 1 | 4 | 4 | 9 | 8785.71 | 291 | 1189357 |
| 1 | 4 | 5 | 1 | 783.10 | 28 | 97770 |
| 1 | 4 | 5 | 2 | 127.17 | 7 | 21026 |
| 1 | 4 | 5 | 3 | 86.26 | 4 | 15583 |
| 1 | 4 | 5 | 4 | 886.11 | 16 | 71474 |
| 1 | 4 | 5 | 5 | 200.68 | 14 | 74804 |
| 1 | 4 | 5 | 6 | 825.58 | 16 | 76879 |
| 1 | 4 | 5 | 7 | 185.36 | 3 | 6085 |
| 1 | 4 | 5 | 8 | 53.05 | 1 | 6827 |
| 1 | 4 | 5 | 9 | 9849.89 | 324 | 1672294 |
| 1 | 4 | 6 | 1 | 1839.13 | 72 | 505590 |
| 1 | 4 | 6 | 2 | 298.73 | 5 | 16182 |
| 1 | 4 | 6 | 3 | 234.01 | 8 | 42369 |
| 1 | 4 | 6 | 4 | 1047.27 | 22 | 147524 |
| 1 | 4 | 6 | 5 | 481.63 | 16 | 70430 |
| 1 | 4 | 6 | 6 | 1317.07 | 34 | 162323 |
| 1 | 4 | 6 | 7 | 360.55 | 9 | 127814 |
| 1 | 4 | 6 | 8 | 90.61 | 7 | 80134 |
| 1 | 4 | 6 | 9 | 17332.90 | 535 | 2833885 |
| 1 | 4 | 7 | 1 | 15297.44 | 389 | 2505764 |
| 1 | 4 | 7 | 2 | 2085.44 | 65 | 296375 |
| 1 | 4 | 7 | 3 | 2140.94 | 38 | 253490 |
| 1 | 4 | 7 | 4 | 6923.74 | 100 | 435674 |
| 1 | 4 | 7 | 5 | 3721.62 | 115 | 641018 |
| 1 | 4 | 7 | 6 | 10409.88 | 194 | 1070372 |
| 1 | 4 | 7 | 7 | 3252.99 | 86 | 317119 |
| 1 | 4 | 7 | 8 | 768.54 | 23 | 160411 |
| 1 | 4 | 7 | 9 | 127687.27 | 2894 | 15540162 |
| 1 | 5 | 1 | 1 | 161.19 | 22 | 112479 |
| 1 | 5 | 1 | 2 | 15.53 | 2 | 1668 |
| 1 | 5 | 1 | 3 | 6.07 | 0 | 0 |
| 1 | 5 | 1 | 4 | 454.21 | 15 | 61507 |
| 1 | 5 | 1 | 5 | 69.38 | 13 | 83497 |
| 1 | 5 | 1 | 6 | 301.14 | 21 | 87734 |
| 1 | 5 | 1 | 7 | 47.82 | 6 | 51950 |
| 1 | 5 | 1 | 8 | 10.84 | 0 | 0 |
| 1 | 5 | 1 | 9 | 3645.26 | 407 | 1855941 |
| 1 | 5 | 2 | 1 | 132.69 | 7 | 27325 |
| 1 | 5 | 2 | 2 | 17.31 | 1 | 1554 |
| 1 | 5 | 2 | 3 | 4.20 | 0 | 0 |
| 1 | 5 | 2 | 4 | 324.26 | 10 | 22854 |
| 1 | 5 | 2 | 5 | 51.80 | 4 | 40692 |
| 1 | 5 | 2 | 6 | 218.84 | 12 | 88266 |
| 1 | 5 | 2 | 7 | 39.68 | 3 | 38808 |
| 1 | 5 | 2 | 8 | 12.15 | 1 | 1029 |
| 1 | 5 | 2 | 9 | 2694.25 | 174 | 616744 |
| 1 | 5 | 3 | 1 | 122.86 | 8 | 51943 |
| 1 | 5 | 3 | 2 | 21.15 | 0 | 0 |
| 1 | 5 | 3 | 3 | 5.15 | 0 | 0 |
| 1 | 5 | 3 | 4 | 240.23 | 6 | 13492 |
| 1 | 5 | 3 | 5 | 38.15 | 6 | 16170 |
| 1 | 5 | 3 | 6 | 173.78 | 4 | 17523 |
| 1 | 5 | 3 | 7 | 30.43 | 2 | 6421 |
| 1 | 5 | 3 | 8 | 4.82 | 1 | 31442 |
| 1 | 5 | 3 | 9 | 1993.33 | 117 | 481752 |
| 1 | 5 | 4 | 1 | 116.24 | 3 | 7229 |
| 1 | 5 | 4 | 2 | 16.48 | 1 | 1000 |
| 1 | 5 | 4 | 3 | 9.31 | 1 | 9867 |
| 1 | 5 | 4 | 4 | 160.66 | 8 | 22404 |
| 1 | 5 | 4 | 5 | 27.77 | 4 | 8119 |
| 1 | 5 | 4 | 6 | 145.54 | 8 | 33299 |
| 1 | 5 | 4 | 7 | 30.23 | 0 | 0 |
| 1 | 5 | 4 | 8 | 7.77 | 1 | 2700 |
| 1 | 5 | 4 | 9 | 1592.59 | 74 | 364037 |
| 1 | 5 | 5 | 1 | 185.95 | 11 | 53110 |
| 1 | 5 | 5 | 2 | 23.75 | 2 | 4900 |
| 1 | 5 | 5 | 3 | 15.57 | 0 | 0 |
| 1 | 5 | 5 | 4 | 140.66 | 2 | 4876 |
| 1 | 5 | 5 | 5 | 41.71 | 1 | 7056 |
| 1 | 5 | 5 | 6 | 141.81 | 2 | 3200 |
| 1 | 5 | 5 | 7 | 44.08 | 3 | 64516 |
| 1 | 5 | 5 | 8 | 9.68 | 0 | 0 |
| 1 | 5 | 5 | 9 | 1752.09 | 86 | 299385 |
| 1 | 5 | 6 | 1 | 394.91 | 9 | 25994 |
| 1 | 5 | 6 | 2 | 55.35 | 3 | 7232 |
| 1 | 5 | 6 | 3 | 40.03 | 1 | 1373 |
| 1 | 5 | 6 | 4 | 177.67 | 4 | 6211 |
| 1 | 5 | 6 | 5 | 92.95 | 7 | 21706 |
| 1 | 5 | 6 | 6 | 244.32 | 8 | 41753 |
| 1 | 5 | 6 | 7 | 92.99 | 5 | 6674 |
| 1 | 5 | 6 | 8 | 22.62 | 2 | 1522 |
| 1 | 5 | 6 | 9 | 3251.89 | 165 | 774028 |
| 1 | 5 | 7 | 1 | 2257.49 | 80 | 452280 |
| 1 | 5 | 7 | 2 | 284.44 | 7 | 45614 |
| 1 | 5 | 7 | 3 | 300.78 | 9 | 55124 |
| 1 | 5 | 7 | 4 | 946.25 | 19 | 68243 |
| 1 | 5 | 7 | 5 | 583.99 | 18 | 113925 |
| 1 | 5 | 7 | 6 | 1332.39 | 38 | 138432 |
| 1 | 5 | 7 | 7 | 541.88 | 13 | 93691 |
| 1 | 5 | 7 | 8 | 125.14 | 5 | 46879 |
| 1 | 5 | 7 | 9 | 17722.19 | 589 | 2700050 |
| 1 | 6 | 1 | 1 | 340.10 | 31 | 75947 |
| 1 | 6 | 1 | 2 | 38.25 | 3 | 5658 |
| 1 | 6 | 1 | 3 | 16.23 | 0 | 0 |
| 1 | 6 | 1 | 4 | 767.66 | 30 | 187167 |
| 1 | 6 | 1 | 5 | 134.82 | 31 | 164961 |
| 1 | 6 | 1 | 6 | 585.23 | 44 | 309679 |
| 1 | 6 | 1 | 7 | 80.16 | 7 | 8237 |
| 1 | 6 | 1 | 8 | 29.87 | 4 | 35088 |
| 1 | 6 | 1 | 9 | 6744.61 | 542 | 2708623 |
| 1 | 6 | 2 | 1 | 233.67 | 20 | 159609 |
| 1 | 6 | 2 | 2 | 33.60 | 2 | 5403 |
| 1 | 6 | 2 | 3 | 14.01 | 0 | 0 |
| 1 | 6 | 2 | 4 | 563.21 | 7 | 12459 |
| 1 | 6 | 2 | 5 | 84.85 | 10 | 55348 |
| 1 | 6 | 2 | 6 | 436.38 | 14 | 72563 |
| 1 | 6 | 2 | 7 | 63.25 | 3 | 63976 |
| 1 | 6 | 2 | 8 | 13.61 | 0 | 0 |
| 1 | 6 | 2 | 9 | 4721.76 | 227 | 970016 |
| 1 | 6 | 3 | 1 | 230.77 | 10 | 97153 |
| 1 | 6 | 3 | 2 | 37.88 | 1 | 789 |
| 1 | 6 | 3 | 3 | 14.41 | 0 | 0 |
| 1 | 6 | 3 | 4 | 386.70 | 10 | 57758 |
| 1 | 6 | 3 | 5 | 76.88 | 5 | 14166 |
| 1 | 6 | 3 | 6 | 294.37 | 15 | 106215 |
| 1 | 6 | 3 | 7 | 57.46 | 3 | 41564 |
| 1 | 6 | 3 | 8 | 12.76 | 0 | 0 |
| 1 | 6 | 3 | 9 | 3558.48 | 131 | 785697 |
| 1 | 6 | 4 | 1 | 186.52 | 12 | 81889 |
| 1 | 6 | 4 | 2 | 31.99 | 3 | 2985 |
| 1 | 6 | 4 | 3 | 15.77 | 0 | 0 |
| 1 | 6 | 4 | 4 | 283.49 | 6 | 73962 |
| 1 | 6 | 4 | 5 | 57.53 | 5 | 20515 |
| 1 | 6 | 4 | 6 | 219.19 | 5 | 14794 |
| 1 | 6 | 4 | 7 | 45.35 | 4 | 38560 |
| 1 | 6 | 4 | 8 | 24.46 | 2 | 3138 |
| 1 | 6 | 4 | 9 | 2708.07 | 99 | 517218 |
| 1 | 6 | 5 | 1 | 253.84 | 20 | 105565 |
| 1 | 6 | 5 | 2 | 47.01 | 2 | 5207 |
| 1 | 6 | 5 | 3 | 28.29 | 0 | 0 |
| 1 | 6 | 5 | 4 | 259.21 | 1 | 31442 |
| 1 | 6 | 5 | 5 | 72.82 | 1 | 1742 |
| 1 | 6 | 5 | 6 | 252.17 | 8 | 74154 |
| 1 | 6 | 5 | 7 | 64.53 | 3 | 8546 |
| 1 | 6 | 5 | 8 | 22.19 | 1 | 2198 |
| 1 | 6 | 5 | 9 | 2936.87 | 87 | 641508 |
| 1 | 6 | 6 | 1 | 560.62 | 17 | 107765 |
| 1 | 6 | 6 | 2 | 88.23 | 0 | 0 |
| 1 | 6 | 6 | 3 | 55.88 | 3 | 4731 |
| 1 | 6 | 6 | 4 | 274.15 | 3 | 10929 |
| 1 | 6 | 6 | 5 | 186.00 | 9 | 16980 |
| 1 | 6 | 6 | 6 | 424.38 | 12 | 62560 |
| 1 | 6 | 6 | 7 | 141.38 | 4 | 39806 |
| 1 | 6 | 6 | 8 | 60.89 | 3 | 4512 |
| 1 | 6 | 6 | 9 | 5248.10 | 187 | 1066083 |
| 1 | 6 | 7 | 1 | 4492.77 | 136 | 727249 |
| 1 | 6 | 7 | 2 | 606.55 | 16 | 114290 |
| 1 | 6 | 7 | 3 | 561.04 | 21 | 128950 |
| 1 | 6 | 7 | 4 | 1799.95 | 29 | 191942 |
| 1 | 6 | 7 | 5 | 1203.92 | 48 | 118462 |
| 1 | 6 | 7 | 6 | 2874.45 | 70 | 422565 |
| 1 | 6 | 7 | 7 | 914.58 | 27 | 208821 |
| 1 | 6 | 7 | 8 | 347.40 | 15 | 131927 |
| 1 | 6 | 7 | 9 | 34969.21 | 886 | 5181284 |
| 1 | 7 | 1 | 1 | 23.96 | 4 | 9848 |
| 1 | 7 | 1 | 2 | 4.05 | 0 | 0 |
| 1 | 7 | 1 | 4 | 92.39 | 5 | 4642 |
| 1 | 7 | 1 | 5 | 7.36 | 0 | 0 |
| 1 | 7 | 1 | 6 | 29.72 | 0 | 0 |
| 1 | 7 | 1 | 7 | 4.29 | 1 | 1504 |
| 1 | 7 | 1 | 8 | 1.04 | 0 | 0 |
| 1 | 7 | 1 | 9 | 560.17 | 38 | 108198 |
| 1 | 7 | 2 | 1 | 20.83 | 1 | 2772 |
| 1 | 7 | 2 | 2 | 3.41 | 0 | 0 |
| 1 | 7 | 2 | 3 | 0.23 | 0 | 0 |
| 1 | 7 | 2 | 4 | 48.63 | 1 | 1980 |
| 1 | 7 | 2 | 5 | 2.10 | 0 | 0 |
| 1 | 7 | 2 | 6 | 20.84 | 5 | 12647 |
| 1 | 7 | 2 | 7 | 2.22 | 0 | 0 |
| 1 | 7 | 2 | 8 | 0.47 | 0 | 0 |
| 1 | 7 | 2 | 9 | 413.54 | 19 | 45789 |
| 1 | 7 | 3 | 1 | 17.42 | 0 | 0 |
| 1 | 7 | 3 | 2 | 2.38 | 0 | 0 |
| 1 | 7 | 3 | 3 | 0.50 | 0 | 0 |
| 1 | 7 | 3 | 4 | 46.18 | 1 | 756 |
| 1 | 7 | 3 | 5 | 3.31 | 0 | 0 |
| 1 | 7 | 3 | 6 | 13.92 | 1 | 2199 |
| 1 | 7 | 3 | 7 | 3.70 | 0 | 0 |
| 1 | 7 | 3 | 8 | 0.30 | 0 | 0 |
| 1 | 7 | 3 | 9 | 285.04 | 7 | 15229 |
| 1 | 7 | 4 | 1 | 13.24 | 0 | 0 |
| 1 | 7 | 4 | 2 | 2.31 | 1 | 5000 |
| 1 | 7 | 4 | 3 | 0.80 | 0 | 0 |
| 1 | 7 | 4 | 4 | 27.66 | 0 | 0 |
| 1 | 7 | 4 | 5 | 4.74 | 0 | 0 |
| 1 | 7 | 4 | 6 | 11.37 | 0 | 0 |
| 1 | 7 | 4 | 7 | 2.64 | 0 | 0 |
| 1 | 7 | 4 | 9 | 225.35 | 5 | 9681 |
| 1 | 7 | 5 | 1 | 19.87 | 0 | 0 |
| 1 | 7 | 5 | 2 | 5.74 | 1 | 3900 |
| 1 | 7 | 5 | 3 | 1.69 | 0 | 0 |
| 1 | 7 | 5 | 4 | 29.05 | 1 | 2913 |
| 1 | 7 | 5 | 5 | 3.59 | 0 | 0 |
| 1 | 7 | 5 | 6 | 14.42 | 1 | 3174 |
| 1 | 7 | 5 | 7 | 2.42 | 0 | 0 |
| 1 | 7 | 5 | 8 | 0.90 | 0 | 0 |
| 1 | 7 | 5 | 9 | 278.75 | 13 | 31522 |
| 1 | 7 | 6 | 1 | 41.17 | 1 | 3325 |
| 1 | 7 | 6 | 2 | 7.55 | 2 | 7963 |
| 1 | 7 | 6 | 3 | 1.56 | 0 | 0 |
| 1 | 7 | 6 | 4 | 36.23 | 1 | 1327 |
| 1 | 7 | 6 | 5 | 9.82 | 0 | 0 |
| 1 | 7 | 6 | 6 | 21.90 | 0 | 0 |
| 1 | 7 | 6 | 7 | 6.58 | 0 | 0 |
| 1 | 7 | 6 | 8 | 0.10 | 0 | 0 |
| 1 | 7 | 6 | 9 | 456.61 | 15 | 103527 |
| 1 | 7 | 7 | 1 | 294.57 | 3 | 8171 |
| 1 | 7 | 7 | 2 | 50.12 | 1 | 1510 |
| 1 | 7 | 7 | 3 | 26.06 | 0 | 0 |
| 1 | 7 | 7 | 4 | 216.41 | 4 | 65435 |
| 1 | 7 | 7 | 5 | 60.68 | 0 | 0 |
| 1 | 7 | 7 | 6 | 208.35 | 5 | 74182 |
| 1 | 7 | 7 | 7 | 46.47 | 0 | 0 |
| 1 | 7 | 7 | 8 | 9.50 | 0 | 0 |
| 1 | 7 | 7 | 9 | 3315.16 | 77 | 340189 |
| 2 | 1 | 1 | 1 | 638.51 | 148 | 578831 |
| 2 | 1 | 1 | 2 | 94.77 | 29 | 137355 |
| 2 | 1 | 1 | 3 | 126.87 | 29 | 137680 |
| 2 | 1 | 1 | 4 | 398.58 | 55 | 162678 |
| 2 | 1 | 1 | 5 | 167.88 | 41 | 73435 |
| 2 | 1 | 1 | 6 | 354.26 | 48 | 166416 |
| 2 | 1 | 1 | 7 | 95.57 | 11 | 21295 |
| 2 | 1 | 1 | 8 | 25.93 | 5 | 2059 |
| 2 | 1 | 1 | 9 | 6792.88 | 1410 | 6556534 |
| 2 | 1 | 2 | 1 | 605.01 | 86 | 484085 |
| 2 | 1 | 2 | 2 | 96.42 | 12 | 93305 |
| 2 | 1 | 2 | 3 | 94.57 | 12 | 62554 |
| 2 | 1 | 2 | 4 | 319.20 | 20 | 43734 |
| 2 | 1 | 2 | 5 | 152.42 | 24 | 109785 |
| 2 | 1 | 2 | 6 | 349.20 | 27 | 92572 |
| 2 | 1 | 2 | 7 | 94.39 | 8 | 76099 |
| 2 | 1 | 2 | 8 | 16.52 | 3 | 39939 |
| 2 | 1 | 2 | 9 | 5941.02 | 722 | 3249461 |
| 2 | 1 | 3 | 1 | 599.51 | 78 | 450864 |
| 2 | 1 | 3 | 2 | 121.49 | 17 | 142141 |
| 2 | 1 | 3 | 3 | 91.96 | 13 | 93038 |
| 2 | 1 | 3 | 4 | 234.48 | 13 | 65170 |
| 2 | 1 | 3 | 5 | 134.82 | 19 | 111059 |
| 2 | 1 | 3 | 6 | 318.69 | 21 | 162284 |
| 2 | 1 | 3 | 7 | 88.04 | 11 | 30153 |
| 2 | 1 | 3 | 8 | 22.47 | 5 | 47551 |
| 2 | 1 | 3 | 9 | 5162.92 | 484 | 2522341 |
| 2 | 1 | 4 | 1 | 597.21 | 55 | 213704 |
| 2 | 1 | 4 | 2 | 129.44 | 7 | 47589 |
| 2 | 1 | 4 | 3 | 94.80 | 9 | 47251 |
| 2 | 1 | 4 | 4 | 182.93 | 12 | 59369 |
| 2 | 1 | 4 | 5 | 111.64 | 11 | 20942 |
| 2 | 1 | 4 | 6 | 263.94 | 9 | 44772 |
| 2 | 1 | 4 | 7 | 107.37 | 9 | 61695 |
| 2 | 1 | 4 | 8 | 23.10 | 3 | 40634 |
| 2 | 1 | 4 | 9 | 4712.87 | 407 | 1631427 |
| 2 | 1 | 5 | 1 | 779.53 | 55 | 232521 |
| 2 | 1 | 5 | 2 | 157.99 | 13 | 31952 |
| 2 | 1 | 5 | 3 | 137.19 | 6 | 50067 |
| 2 | 1 | 5 | 4 | 156.34 | 11 | 18221 |
| 2 | 1 | 5 | 5 | 149.71 | 15 | 32164 |
| 2 | 1 | 5 | 6 | 295.12 | 13 | 59509 |
| 2 | 1 | 5 | 7 | 132.79 | 8 | 55603 |
| 2 | 1 | 5 | 8 | 29.02 | 2 | 2802 |
| 2 | 1 | 5 | 9 | 5373.06 | 363 | 1597528 |
| 2 | 1 | 6 | 1 | 1557.98 | 107 | 435444 |
| 2 | 1 | 6 | 2 | 329.74 | 29 | 133272 |
| 2 | 1 | 6 | 3 | 320.71 | 13 | 150031 |
| 2 | 1 | 6 | 4 | 210.91 | 4 | 15193 |
| 2 | 1 | 6 | 5 | 336.02 | 30 | 194477 |
| 2 | 1 | 6 | 6 | 576.63 | 24 | 137963 |
| 2 | 1 | 6 | 7 | 269.81 | 9 | 87411 |
| 2 | 1 | 6 | 8 | 56.96 | 9 | 144950 |
| 2 | 1 | 6 | 9 | 9805.53 | 618 | 2918359 |
| 2 | 1 | 7 | 1 | 8009.92 | 390 | 1992027 |
| 2 | 1 | 7 | 2 | 1407.85 | 67 | 332194 |
| 2 | 1 | 7 | 3 | 1538.74 | 49 | 397236 |
| 2 | 1 | 7 | 4 | 806.00 | 31 | 209824 |
| 2 | 1 | 7 | 5 | 1380.85 | 83 | 398103 |
| 2 | 1 | 7 | 6 | 2848.53 | 111 | 493340 |
| 2 | 1 | 7 | 7 | 1496.62 | 74 | 282000 |
| 2 | 1 | 7 | 8 | 267.80 | 14 | 95457 |
| 2 | 1 | 7 | 9 | 44511.41 | 2127 | 10315455 |
| 2 | 2 | 1 | 1 | 679.46 | 113 | 582788 |
| 2 | 2 | 1 | 2 | 98.43 | 22 | 91135 |
| 2 | 2 | 1 | 3 | 60.48 | 11 | 90425 |
| 2 | 2 | 1 | 4 | 434.05 | 45 | 153794 |
| 2 | 2 | 1 | 5 | 211.77 | 34 | 255298 |
| 2 | 2 | 1 | 6 | 516.01 | 51 | 253258 |
| 2 | 2 | 1 | 7 | 118.76 | 16 | 69025 |
| 2 | 2 | 1 | 8 | 25.01 | 5 | 7797 |
| 2 | 2 | 1 | 9 | 7185.14 | 1157 | 5121951 |
| 2 | 2 | 2 | 1 | 638.08 | 83 | 350944 |
| 2 | 2 | 2 | 2 | 117.12 | 19 | 141774 |
| 2 | 2 | 2 | 3 | 52.69 | 11 | 58588 |
| 2 | 2 | 2 | 4 | 408.69 | 22 | 136288 |
| 2 | 2 | 2 | 5 | 168.09 | 33 | 150740 |
| 2 | 2 | 2 | 6 | 523.36 | 22 | 100822 |
| 2 | 2 | 2 | 7 | 141.28 | 15 | 57916 |
| 2 | 2 | 2 | 8 | 25.84 | 5 | 42167 |
| 2 | 2 | 2 | 9 | 6506.72 | 559 | 2457197 |
| 2 | 2 | 3 | 1 | 687.29 | 60 | 382872 |
| 2 | 2 | 3 | 2 | 111.63 | 11 | 55353 |
| 2 | 2 | 3 | 3 | 68.91 | 5 | 7480 |
| 2 | 2 | 3 | 4 | 294.06 | 14 | 88500 |
| 2 | 2 | 3 | 5 | 154.39 | 20 | 42607 |
| 2 | 2 | 3 | 6 | 446.83 | 25 | 116227 |
| 2 | 2 | 3 | 7 | 139.62 | 9 | 18627 |
| 2 | 2 | 3 | 8 | 28.91 | 2 | 4521 |
| 2 | 2 | 3 | 9 | 5783.55 | 453 | 1907609 |
| 2 | 2 | 4 | 1 | 661.35 | 50 | 257851 |
| 2 | 2 | 4 | 2 | 139.58 | 15 | 29492 |
| 2 | 2 | 4 | 3 | 67.99 | 3 | 4835 |
| 2 | 2 | 4 | 4 | 198.46 | 6 | 11144 |
| 2 | 2 | 4 | 5 | 151.85 | 10 | 18943 |
| 2 | 2 | 4 | 6 | 390.18 | 15 | 37755 |
| 2 | 2 | 4 | 7 | 120.11 | 9 | 55231 |
| 2 | 2 | 4 | 8 | 33.10 | 1 | 1878 |
| 2 | 2 | 4 | 9 | 5316.84 | 344 | 1682243 |
| 2 | 2 | 5 | 1 | 848.62 | 70 | 265184 |
| 2 | 2 | 5 | 2 | 204.12 | 19 | 116076 |
| 2 | 2 | 5 | 3 | 129.16 | 6 | 20054 |
| 2 | 2 | 5 | 4 | 149.52 | 7 | 40010 |
| 2 | 2 | 5 | 5 | 214.27 | 14 | 21497 |
| 2 | 2 | 5 | 6 | 431.35 | 18 | 89520 |
| 2 | 2 | 5 | 7 | 176.70 | 10 | 25944 |
| 2 | 2 | 5 | 8 | 50.75 | 3 | 10388 |
| 2 | 2 | 5 | 9 | 6273.26 | 344 | 1437097 |
| 2 | 2 | 6 | 1 | 1741.30 | 99 | 502889 |
| 2 | 2 | 6 | 2 | 358.55 | 22 | 108381 |
| 2 | 2 | 6 | 3 | 286.92 | 14 | 49960 |
| 2 | 2 | 6 | 4 | 192.90 | 7 | 11847 |
| 2 | 2 | 6 | 5 | 398.56 | 21 | 135284 |
| 2 | 2 | 6 | 6 | 710.28 | 32 | 75776 |
| 2 | 2 | 6 | 7 | 356.80 | 12 | 25779 |
| 2 | 2 | 6 | 8 | 103.30 | 9 | 27406 |
| 2 | 2 | 6 | 9 | 11001.90 | 622 | 3029300 |
| 2 | 2 | 7 | 1 | 9358.84 | 359 | 2466406 |
| 2 | 2 | 7 | 2 | 2021.95 | 107 | 520377 |
| 2 | 2 | 7 | 3 | 1795.27 | 53 | 328548 |
| 2 | 2 | 7 | 4 | 859.65 | 23 | 95241 |
| 2 | 2 | 7 | 5 | 1856.01 | 77 | 323882 |
| 2 | 2 | 7 | 6 | 3817.88 | 96 | 503384 |
| 2 | 2 | 7 | 7 | 2125.92 | 91 | 463818 |
| 2 | 2 | 7 | 8 | 407.26 | 10 | 89166 |
| 2 | 2 | 7 | 9 | 54421.40 | 2087 | 9950131 |
| 2 | 3 | 1 | 1 | 703.88 | 120 | 547349 |
| 2 | 3 | 1 | 2 | 88.45 | 10 | 20304 |
| 2 | 3 | 1 | 3 | 39.68 | 3 | 5422 |
| 2 | 3 | 1 | 4 | 461.44 | 33 | 121470 |
| 2 | 3 | 1 | 5 | 209.99 | 53 | 234736 |
| 2 | 3 | 1 | 6 | 633.85 | 52 | 241224 |
| 2 | 3 | 1 | 7 | 142.00 | 14 | 68256 |
| 2 | 3 | 1 | 8 | 23.45 | 2 | 8396 |
| 2 | 3 | 1 | 9 | 7304.73 | 1003 | 4387841 |
| 2 | 3 | 2 | 1 | 700.59 | 74 | 286946 |
| 2 | 3 | 2 | 2 | 96.84 | 7 | 20675 |
| 2 | 3 | 2 | 3 | 44.37 | 1 | 31442 |
| 2 | 3 | 2 | 4 | 422.88 | 17 | 14982 |
| 2 | 3 | 2 | 5 | 177.47 | 27 | 154791 |
| 2 | 3 | 2 | 6 | 669.34 | 42 | 114629 |
| 2 | 3 | 2 | 7 | 151.12 | 17 | 36169 |
| 2 | 3 | 2 | 8 | 27.39 | 1 | 31442 |
| 2 | 3 | 2 | 9 | 6988.90 | 556 | 2634269 |
| 2 | 3 | 3 | 1 | 724.49 | 49 | 189534 |
| 2 | 3 | 3 | 2 | 121.33 | 9 | 32584 |
| 2 | 3 | 3 | 3 | 55.59 | 0 | 0 |
| 2 | 3 | 3 | 4 | 275.90 | 7 | 40454 |
| 2 | 3 | 3 | 5 | 162.92 | 17 | 33909 |
| 2 | 3 | 3 | 6 | 576.10 | 21 | 55806 |
| 2 | 3 | 3 | 7 | 140.05 | 13 | 76834 |
| 2 | 3 | 3 | 8 | 36.78 | 0 | 0 |
| 2 | 3 | 3 | 9 | 6034.63 | 404 | 2107152 |
| 2 | 3 | 4 | 1 | 679.01 | 38 | 197187 |
| 2 | 3 | 4 | 2 | 119.96 | 13 | 62674 |
| 2 | 3 | 4 | 3 | 69.04 | 2 | 2597 |
| 2 | 3 | 4 | 4 | 173.48 | 11 | 46956 |
| 2 | 3 | 4 | 5 | 155.48 | 8 | 45486 |
| 2 | 3 | 4 | 6 | 468.53 | 19 | 75634 |
| 2 | 3 | 4 | 7 | 147.89 | 9 | 84248 |
| 2 | 3 | 4 | 8 | 41.40 | 4 | 35685 |
| 2 | 3 | 4 | 9 | 5496.81 | 323 | 1473149 |
| 2 | 3 | 5 | 1 | 946.01 | 50 | 199324 |
| 2 | 3 | 5 | 2 | 172.42 | 12 | 27067 |
| 2 | 3 | 5 | 3 | 104.52 | 4 | 34911 |
| 2 | 3 | 5 | 4 | 188.53 | 4 | 33175 |
| 2 | 3 | 5 | 5 | 209.61 | 9 | 81779 |
| 2 | 3 | 5 | 6 | 515.69 | 17 | 77953 |
| 2 | 3 | 5 | 7 | 189.16 | 10 | 21942 |
| 2 | 3 | 5 | 8 | 55.80 | 6 | 23456 |
| 2 | 3 | 5 | 9 | 6442.14 | 324 | 1506141 |
| 2 | 3 | 6 | 1 | 1702.76 | 86 | 491502 |
| 2 | 3 | 6 | 2 | 332.17 | 10 | 21654 |
| 2 | 3 | 6 | 3 | 306.21 | 11 | 72861 |
| 2 | 3 | 6 | 4 | 193.65 | 6 | 11444 |
| 2 | 3 | 6 | 5 | 452.37 | 30 | 201310 |
| 2 | 3 | 6 | 6 | 834.26 | 38 | 182641 |
| 2 | 3 | 6 | 7 | 367.00 | 17 | 76297 |
| 2 | 3 | 6 | 8 | 126.83 | 8 | 27834 |
| 2 | 3 | 6 | 9 | 10730.07 | 492 | 2038707 |
| 2 | 3 | 7 | 1 | 10469.92 | 325 | 1401833 |
| 2 | 3 | 7 | 2 | 2071.24 | 68 | 353788 |
| 2 | 3 | 7 | 3 | 2180.19 | 59 | 324185 |
| 2 | 3 | 7 | 4 | 917.17 | 19 | 73569 |
| 2 | 3 | 7 | 5 | 2435.19 | 86 | 468488 |
| 2 | 3 | 7 | 6 | 4857.97 | 121 | 605098 |
| 2 | 3 | 7 | 7 | 2416.40 | 83 | 349608 |
| 2 | 3 | 7 | 8 | 704.42 | 22 | 134382 |
| 2 | 3 | 7 | 9 | 60140.20 | 2044 | 10518198 |
| 2 | 4 | 1 | 1 | 1493.99 | 226 | 1107859 |
| 2 | 4 | 1 | 2 | 131.48 | 14 | 103393 |
| 2 | 4 | 1 | 3 | 88.79 | 8 | 112948 |
| 2 | 4 | 1 | 4 | 774.10 | 39 | 121494 |
| 2 | 4 | 1 | 5 | 372.41 | 66 | 369471 |
| 2 | 4 | 1 | 6 | 1295.44 | 109 | 492597 |
| 2 | 4 | 1 | 7 | 240.77 | 23 | 51380 |
| 2 | 4 | 1 | 8 | 44.59 | 8 | 20312 |
| 2 | 4 | 1 | 9 | 13502.14 | 1442 | 7243260 |
| 2 | 4 | 2 | 1 | 1402.82 | 119 | 614064 |
| 2 | 4 | 2 | 2 | 157.16 | 13 | 37643 |
| 2 | 4 | 2 | 3 | 87.93 | 4 | 16203 |
| 2 | 4 | 2 | 4 | 727.28 | 35 | 212362 |
| 2 | 4 | 2 | 5 | 317.39 | 38 | 204612 |
| 2 | 4 | 2 | 6 | 1299.16 | 65 | 566535 |
| 2 | 4 | 2 | 7 | 250.94 | 18 | 128549 |
| 2 | 4 | 2 | 8 | 52.96 | 5 | 35588 |
| 2 | 4 | 2 | 9 | 12692.50 | 849 | 4327298 |
| 2 | 4 | 3 | 1 | 1388.66 | 99 | 691234 |
| 2 | 4 | 3 | 2 | 177.33 | 5 | 45982 |
| 2 | 4 | 3 | 3 | 107.04 | 4 | 14953 |
| 2 | 4 | 3 | 4 | 497.40 | 15 | 38416 |
| 2 | 4 | 3 | 5 | 280.10 | 23 | 235331 |
| 2 | 4 | 3 | 6 | 1084.19 | 46 | 166621 |
| 2 | 4 | 3 | 7 | 246.24 | 10 | 35221 |
| 2 | 4 | 3 | 8 | 61.36 | 6 | 83511 |
| 2 | 4 | 3 | 9 | 10957.97 | 580 | 3353774 |
| 2 | 4 | 4 | 1 | 1335.57 | 82 | 358249 |
| 2 | 4 | 4 | 2 | 229.51 | 8 | 18246 |
| 2 | 4 | 4 | 3 | 126.18 | 2 | 1916 |
| 2 | 4 | 4 | 4 | 364.11 | 11 | 34707 |
| 2 | 4 | 4 | 5 | 318.83 | 12 | 40334 |
| 2 | 4 | 4 | 6 | 873.94 | 33 | 170727 |
| 2 | 4 | 4 | 7 | 241.30 | 12 | 86801 |
| 2 | 4 | 4 | 8 | 76.90 | 4 | 19358 |
| 2 | 4 | 4 | 9 | 9689.88 | 445 | 2107274 |
| 2 | 4 | 5 | 1 | 1685.23 | 82 | 547932 |
| 2 | 4 | 5 | 2 | 323.48 | 15 | 38665 |
| 2 | 4 | 5 | 3 | 223.59 | 5 | 16820 |
| 2 | 4 | 5 | 4 | 349.22 | 3 | 6779 |
| 2 | 4 | 5 | 5 | 390.21 | 15 | 161309 |
| 2 | 4 | 5 | 6 | 986.77 | 31 | 230920 |
| 2 | 4 | 5 | 7 | 329.99 | 8 | 51133 |
| 2 | 4 | 5 | 8 | 115.65 | 5 | 25988 |
| 2 | 4 | 5 | 9 | 10932.73 | 441 | 2172831 |
| 2 | 4 | 6 | 1 | 3057.73 | 116 | 579356 |
| 2 | 4 | 6 | 2 | 665.09 | 29 | 142262 |
| 2 | 4 | 6 | 3 | 570.12 | 18 | 110476 |
| 2 | 4 | 6 | 4 | 347.66 | 10 | 62709 |
| 2 | 4 | 6 | 5 | 722.62 | 37 | 134350 |
| 2 | 4 | 6 | 6 | 1508.43 | 41 | 206813 |
| 2 | 4 | 6 | 7 | 656.37 | 17 | 45923 |
| 2 | 4 | 6 | 8 | 259.31 | 13 | 74790 |
| 2 | 4 | 6 | 9 | 19012.21 | 728 | 3816718 |
| 2 | 4 | 7 | 1 | 21848.06 | 605 | 3502535 |
| 2 | 4 | 7 | 2 | 4430.43 | 153 | 836130 |
| 2 | 4 | 7 | 3 | 4695.14 | 91 | 528367 |
| 2 | 4 | 7 | 4 | 1818.17 | 33 | 101358 |
| 2 | 4 | 7 | 5 | 4808.39 | 127 | 850044 |
| 2 | 4 | 7 | 6 | 10510.83 | 242 | 1174270 |
| 2 | 4 | 7 | 7 | 4635.35 | 135 | 697806 |
| 2 | 4 | 7 | 8 | 1853.07 | 49 | 319803 |
| 2 | 4 | 7 | 9 | 121293.07 | 3338 | 18245026 |
| 2 | 5 | 1 | 1 | 217.27 | 47 | 161646 |
| 2 | 5 | 1 | 2 | 24.81 | 1 | 4656 |
| 2 | 5 | 1 | 3 | 14.58 | 1 | 2810 |
| 2 | 5 | 1 | 4 | 96.11 | 4 | 43315 |
| 2 | 5 | 1 | 5 | 58.14 | 13 | 32595 |
| 2 | 5 | 1 | 6 | 182.69 | 15 | 61055 |
| 2 | 5 | 1 | 7 | 40.30 | 5 | 35437 |
| 2 | 5 | 1 | 8 | 5.82 | 2 | 6656 |
| 2 | 5 | 1 | 9 | 1933.36 | 250 | 1001018 |
| 2 | 5 | 2 | 1 | 211.17 | 20 | 113635 |
| 2 | 5 | 2 | 2 | 27.01 | 5 | 39053 |
| 2 | 5 | 2 | 3 | 11.46 | 0 | 0 |
| 2 | 5 | 2 | 4 | 89.19 | 4 | 23893 |
| 2 | 5 | 2 | 5 | 58.24 | 10 | 24691 |
| 2 | 5 | 2 | 6 | 208.24 | 12 | 29123 |
| 2 | 5 | 2 | 7 | 56.58 | 2 | 1758 |
| 2 | 5 | 2 | 8 | 8.09 | 1 | 4834 |
| 2 | 5 | 2 | 9 | 1976.19 | 176 | 1044585 |
| 2 | 5 | 3 | 1 | 231.22 | 23 | 64911 |
| 2 | 5 | 3 | 2 | 32.05 | 1 | 2536 |
| 2 | 5 | 3 | 3 | 14.51 | 2 | 1453 |
| 2 | 5 | 3 | 4 | 56.66 | 3 | 5473 |
| 2 | 5 | 3 | 5 | 48.09 | 7 | 8258 |
| 2 | 5 | 3 | 6 | 175.31 | 7 | 16559 |
| 2 | 5 | 3 | 7 | 46.96 | 4 | 7541 |
| 2 | 5 | 3 | 8 | 12.26 | 0 | 0 |
| 2 | 5 | 3 | 9 | 1710.73 | 101 | 352227 |
| 2 | 5 | 4 | 1 | 229.87 | 16 | 70312 |
| 2 | 5 | 4 | 2 | 30.72 | 1 | 963 |
| 2 | 5 | 4 | 3 | 17.05 | 1 | 2320 |
| 2 | 5 | 4 | 4 | 35.98 | 1 | 2762 |
| 2 | 5 | 4 | 5 | 51.82 | 4 | 37247 |
| 2 | 5 | 4 | 6 | 151.72 | 7 | 16448 |
| 2 | 5 | 4 | 7 | 50.32 | 5 | 17564 |
| 2 | 5 | 4 | 8 | 11.86 | 2 | 36323 |
| 2 | 5 | 4 | 9 | 1513.60 | 94 | 391430 |
| 2 | 5 | 5 | 1 | 290.33 | 17 | 99863 |
| 2 | 5 | 5 | 2 | 56.82 | 2 | 9871 |
| 2 | 5 | 5 | 3 | 32.05 | 0 | 0 |
| 2 | 5 | 5 | 4 | 41.54 | 0 | 0 |
| 2 | 5 | 5 | 5 | 77.17 | 5 | 49022 |
| 2 | 5 | 5 | 6 | 167.47 | 7 | 20196 |
| 2 | 5 | 5 | 7 | 81.90 | 6 | 72912 |
| 2 | 5 | 5 | 8 | 28.40 | 2 | 8215 |
| 2 | 5 | 5 | 9 | 1872.74 | 116 | 725258 |
| 2 | 5 | 6 | 1 | 608.43 | 29 | 81371 |
| 2 | 5 | 6 | 2 | 128.85 | 8 | 16730 |
| 2 | 5 | 6 | 3 | 96.56 | 3 | 13046 |
| 2 | 5 | 6 | 4 | 43.29 | 1 | 390 |
| 2 | 5 | 6 | 5 | 149.80 | 7 | 12686 |
| 2 | 5 | 6 | 6 | 265.29 | 11 | 45599 |
| 2 | 5 | 6 | 7 | 135.47 | 16 | 41245 |
| 2 | 5 | 6 | 8 | 55.22 | 6 | 70624 |
| 2 | 5 | 6 | 9 | 3457.83 | 162 | 764745 |
| 2 | 5 | 7 | 1 | 3359.90 | 122 | 604369 |
| 2 | 5 | 7 | 2 | 606.13 | 27 | 142803 |
| 2 | 5 | 7 | 3 | 610.72 | 16 | 109950 |
| 2 | 5 | 7 | 4 | 207.66 | 6 | 36294 |
| 2 | 5 | 7 | 5 | 728.55 | 34 | 120719 |
| 2 | 5 | 7 | 6 | 1353.85 | 50 | 293518 |
| 2 | 5 | 7 | 7 | 736.44 | 18 | 47691 |
| 2 | 5 | 7 | 8 | 257.73 | 7 | 51190 |
| 2 | 5 | 7 | 9 | 16948.62 | 616 | 3131530 |
| 2 | 6 | 1 | 1 | 572.91 | 85 | 404731 |
| 2 | 6 | 1 | 2 | 44.41 | 2 | 2524 |
| 2 | 6 | 1 | 3 | 23.13 | 1 | 5192 |
| 2 | 6 | 1 | 4 | 197.50 | 8 | 46327 |
| 2 | 6 | 1 | 5 | 138.07 | 19 | 118047 |
| 2 | 6 | 1 | 6 | 444.98 | 50 | 355284 |
| 2 | 6 | 1 | 7 | 84.17 | 14 | 66584 |
| 2 | 6 | 1 | 8 | 30.55 | 3 | 5871 |
| 2 | 6 | 1 | 9 | 4295.20 | 484 | 2540690 |
| 2 | 6 | 2 | 1 | 503.20 | 51 | 272422 |
| 2 | 6 | 2 | 2 | 54.76 | 3 | 7805 |
| 2 | 6 | 2 | 3 | 20.94 | 0 | 0 |
| 2 | 6 | 2 | 4 | 155.64 | 8 | 54065 |
| 2 | 6 | 2 | 5 | 121.24 | 14 | 77633 |
| 2 | 6 | 2 | 6 | 455.65 | 33 | 155704 |
| 2 | 6 | 2 | 7 | 86.44 | 4 | 7725 |
| 2 | 6 | 2 | 8 | 35.30 | 3 | 44018 |
| 2 | 6 | 2 | 9 | 3990.80 | 284 | 1423093 |
| 2 | 6 | 3 | 1 | 507.75 | 35 | 169303 |
| 2 | 6 | 3 | 2 | 55.57 | 1 | 8610 |
| 2 | 6 | 3 | 3 | 22.76 | 0 | 0 |
| 2 | 6 | 3 | 4 | 106.79 | 3 | 6486 |
| 2 | 6 | 3 | 5 | 104.27 | 7 | 18043 |
| 2 | 6 | 3 | 6 | 372.07 | 10 | 53188 |
| 2 | 6 | 3 | 7 | 76.26 | 3 | 4736 |
| 2 | 6 | 3 | 8 | 35.48 | 2 | 2289 |
| 2 | 6 | 3 | 9 | 3470.02 | 224 | 1013321 |
| 2 | 6 | 4 | 1 | 455.00 | 23 | 67152 |
| 2 | 6 | 4 | 2 | 70.27 | 3 | 6864 |
| 2 | 6 | 4 | 3 | 28.52 | 0 | 0 |
| 2 | 6 | 4 | 4 | 92.99 | 2 | 32158 |
| 2 | 6 | 4 | 5 | 89.64 | 3 | 4864 |
| 2 | 6 | 4 | 6 | 285.72 | 10 | 49974 |
| 2 | 6 | 4 | 7 | 90.15 | 5 | 54362 |
| 2 | 6 | 4 | 8 | 42.98 | 3 | 6623 |
| 2 | 6 | 4 | 9 | 2926.50 | 138 | 597450 |
| 2 | 6 | 5 | 1 | 518.47 | 21 | 118651 |
| 2 | 6 | 5 | 2 | 96.83 | 4 | 9580 |
| 2 | 6 | 5 | 3 | 58.16 | 1 | 3521 |
| 2 | 6 | 5 | 4 | 77.26 | 0 | 0 |
| 2 | 6 | 5 | 5 | 122.15 | 12 | 40820 |
| 2 | 6 | 5 | 6 | 301.84 | 9 | 81184 |
| 2 | 6 | 5 | 7 | 100.55 | 5 | 11208 |
| 2 | 6 | 5 | 8 | 66.47 | 4 | 39787 |
| 2 | 6 | 5 | 9 | 3279.28 | 146 | 756142 |
| 2 | 6 | 6 | 1 | 992.33 | 44 | 278171 |
| 2 | 6 | 6 | 2 | 209.98 | 6 | 71372 |
| 2 | 6 | 6 | 3 | 165.79 | 4 | 55283 |
| 2 | 6 | 6 | 4 | 80.16 | 4 | 10539 |
| 2 | 6 | 6 | 5 | 247.97 | 11 | 86405 |
| 2 | 6 | 6 | 6 | 546.95 | 24 | 80714 |
| 2 | 6 | 6 | 7 | 199.47 | 4 | 9307 |
| 2 | 6 | 6 | 8 | 137.44 | 5 | 40319 |
| 2 | 6 | 6 | 9 | 5716.97 | 211 | 1097124 |
| 2 | 6 | 7 | 1 | 6871.94 | 219 | 1148035 |
| 2 | 6 | 7 | 2 | 1358.02 | 47 | 177092 |
| 2 | 6 | 7 | 3 | 1305.97 | 25 | 142010 |
| 2 | 6 | 7 | 4 | 417.82 | 9 | 19434 |
| 2 | 6 | 7 | 5 | 1507.58 | 51 | 233769 |
| 2 | 6 | 7 | 6 | 3172.45 | 55 | 321914 |
| 2 | 6 | 7 | 7 | 1369.78 | 54 | 391112 |
| 2 | 6 | 7 | 8 | 792.12 | 24 | 127778 |
| 2 | 6 | 7 | 9 | 35319.16 | 1037 | 5765190 |
| 2 | 7 | 1 | 1 | 36.94 | 6 | 15613 |
| 2 | 7 | 1 | 2 | 3.06 | 0 | 0 |
| 2 | 7 | 1 | 3 | 2.02 | 0 | 0 |
| 2 | 7 | 1 | 4 | 28.33 | 1 | 3005 |
| 2 | 7 | 1 | 5 | 9.02 | 0 | 0 |
| 2 | 7 | 1 | 6 | 20.84 | 4 | 5072 |
| 2 | 7 | 1 | 7 | 4.48 | 0 | 0 |
| 2 | 7 | 1 | 8 | 1.68 | 0 | 0 |
| 2 | 7 | 1 | 9 | 342.29 | 26 | 157981 |
| 2 | 7 | 2 | 1 | 33.57 | 3 | 6068 |
| 2 | 7 | 2 | 2 | 9.92 | 0 | 0 |
| 2 | 7 | 2 | 3 | 1.30 | 0 | 0 |
| 2 | 7 | 2 | 4 | 22.69 | 1 | 1410 |
| 2 | 7 | 2 | 5 | 10.46 | 2 | 33342 |
| 2 | 7 | 2 | 6 | 24.96 | 1 | 4059 |
| 2 | 7 | 2 | 7 | 5.10 | 0 | 0 |
| 2 | 7 | 2 | 8 | 3.26 | 0 | 0 |
| 2 | 7 | 2 | 9 | 349.42 | 15 | 145126 |
| 2 | 7 | 3 | 1 | 35.15 | 1 | 2200 |
| 2 | 7 | 3 | 2 | 8.06 | 0 | 0 |
| 2 | 7 | 3 | 3 | 1.96 | 0 | 0 |
| 2 | 7 | 3 | 4 | 18.80 | 1 | 1588 |
| 2 | 7 | 3 | 5 | 5.05 | 0 | 0 |
| 2 | 7 | 3 | 6 | 18.54 | 1 | 31442 |
| 2 | 7 | 3 | 7 | 8.40 | 1 | 2800 |
| 2 | 7 | 3 | 8 | 0.35 | 0 | 0 |
| 2 | 7 | 3 | 9 | 292.05 | 13 | 23491 |
| 2 | 7 | 4 | 1 | 27.49 | 1 | 1329 |
| 2 | 7 | 4 | 2 | 4.95 | 0 | 0 |
| 2 | 7 | 4 | 3 | 2.11 | 0 | 0 |
| 2 | 7 | 4 | 4 | 8.96 | 0 | 0 |
| 2 | 7 | 4 | 5 | 6.14 | 1 | 1916 |
| 2 | 7 | 4 | 6 | 17.98 | 0 | 0 |
| 2 | 7 | 4 | 7 | 2.68 | 0 | 0 |
| 2 | 7 | 4 | 8 | 1.64 | 0 | 0 |
| 2 | 7 | 4 | 9 | 258.15 | 5 | 15880 |
| 2 | 7 | 5 | 1 | 38.56 | 3 | 12590 |
| 2 | 7 | 5 | 2 | 10.75 | 0 | 0 |
| 2 | 7 | 5 | 3 | 3.11 | 0 | 0 |
| 2 | 7 | 5 | 4 | 8.92 | 0 | 0 |
| 2 | 7 | 5 | 5 | 4.96 | 0 | 0 |
| 2 | 7 | 5 | 6 | 17.21 | 0 | 0 |
| 2 | 7 | 5 | 7 | 6.31 | 0 | 0 |
| 2 | 7 | 5 | 8 | 2.50 | 0 | 0 |
| 2 | 7 | 5 | 9 | 267.12 | 8 | 11642 |
| 2 | 7 | 6 | 1 | 63.98 | 2 | 6574 |
| 2 | 7 | 6 | 2 | 16.87 | 4 | 7333 |
| 2 | 7 | 6 | 3 | 6.90 | 0 | 0 |
| 2 | 7 | 6 | 4 | 8.68 | 0 | 0 |
| 2 | 7 | 6 | 5 | 11.99 | 0 | 0 |
| 2 | 7 | 6 | 6 | 24.08 | 0 | 0 |
| 2 | 7 | 6 | 7 | 13.38 | 0 | 0 |
| 2 | 7 | 6 | 8 | 6.54 | 0 | 0 |
| 2 | 7 | 6 | 9 | 453.04 | 9 | 81464 |
| 2 | 7 | 7 | 1 | 420.95 | 7 | 16802 |
| 2 | 7 | 7 | 2 | 126.12 | 1 | 6020 |
| 2 | 7 | 7 | 3 | 39.14 | 1 | 1012 |
| 2 | 7 | 7 | 4 | 59.08 | 1 | 3580 |
| 2 | 7 | 7 | 5 | 81.78 | 3 | 3065 |
| 2 | 7 | 7 | 6 | 193.89 | 3 | 32827 |
| 2 | 7 | 7 | 7 | 71.27 | 1 | 603 |
| 2 | 7 | 7 | 8 | 31.36 | 1 | 1021 |
| 2 | 7 | 7 | 9 | 2873.70 | 69 | 381570 |
| 3 | 1 | 1 | 1 | 213.38 | 53 | 244561 |
| 3 | 1 | 1 | 2 | 76.97 | 26 | 187544 |
| 3 | 1 | 1 | 3 | 60.42 | 8 | 18624 |
| 3 | 1 | 1 | 4 | 60.89 | 10 | 81052 |
| 3 | 1 | 1 | 5 | 53.30 | 10 | 52745 |
| 3 | 1 | 1 | 6 | 104.58 | 13 | 168471 |
| 3 | 1 | 1 | 7 | 24.92 | 4 | 5100 |
| 3 | 1 | 1 | 8 | 12.91 | 3 | 42372 |
| 3 | 1 | 1 | 9 | 2375.34 | 456 | 1911772 |
| 3 | 1 | 2 | 1 | 276.13 | 28 | 106668 |
| 3 | 1 | 2 | 2 | 73.41 | 14 | 30232 |
| 3 | 1 | 2 | 3 | 69.26 | 14 | 61941 |
| 3 | 1 | 2 | 4 | 73.29 | 5 | 66851 |
| 3 | 1 | 2 | 5 | 52.25 | 7 | 57304 |
| 3 | 1 | 2 | 6 | 139.64 | 9 | 59193 |
| 3 | 1 | 2 | 7 | 42.93 | 3 | 5646 |
| 3 | 1 | 2 | 8 | 13.03 | 0 | 0 |
| 3 | 1 | 2 | 9 | 2472.22 | 297 | 1413344 |
| 3 | 1 | 3 | 1 | 299.10 | 36 | 196119 |
| 3 | 1 | 3 | 2 | 87.60 | 11 | 55966 |
| 3 | 1 | 3 | 3 | 67.91 | 6 | 13026 |
| 3 | 1 | 3 | 4 | 65.39 | 2 | 2186 |
| 3 | 1 | 3 | 5 | 60.44 | 8 | 23091 |
| 3 | 1 | 3 | 6 | 135.85 | 6 | 74018 |
| 3 | 1 | 3 | 7 | 48.67 | 2 | 3044 |
| 3 | 1 | 3 | 8 | 16.35 | 3 | 12589 |
| 3 | 1 | 3 | 9 | 2411.79 | 256 | 1266725 |
| 3 | 1 | 4 | 1 | 336.16 | 29 | 98220 |
| 3 | 1 | 4 | 2 | 119.03 | 9 | 61145 |
| 3 | 1 | 4 | 3 | 75.71 | 3 | 16285 |
| 3 | 1 | 4 | 4 | 44.78 | 0 | 0 |
| 3 | 1 | 4 | 5 | 69.52 | 11 | 67180 |
| 3 | 1 | 4 | 6 | 115.91 | 10 | 25912 |
| 3 | 1 | 4 | 7 | 59.11 | 2 | 3783 |
| 3 | 1 | 4 | 8 | 18.65 | 0 | 0 |
| 3 | 1 | 4 | 9 | 2419.59 | 209 | 905418 |
| 3 | 1 | 5 | 1 | 480.43 | 41 | 129476 |
| 3 | 1 | 5 | 2 | 164.22 | 16 | 133759 |
| 3 | 1 | 5 | 3 | 123.44 | 7 | 48811 |
| 3 | 1 | 5 | 4 | 50.82 | 2 | 4868 |
| 3 | 1 | 5 | 5 | 102.56 | 3 | 13127 |
| 3 | 1 | 5 | 6 | 159.79 | 15 | 44864 |
| 3 | 1 | 5 | 7 | 73.37 | 9 | 56128 |
| 3 | 1 | 5 | 8 | 32.92 | 2 | 1512 |
| 3 | 1 | 5 | 9 | 3214.83 | 274 | 1088795 |
| 3 | 1 | 6 | 1 | 1110.72 | 84 | 399470 |
| 3 | 1 | 6 | 2 | 327.30 | 32 | 100742 |
| 3 | 1 | 6 | 3 | 300.23 | 47 | 234344 |
| 3 | 1 | 6 | 4 | 52.79 | 2 | 6842 |
| 3 | 1 | 6 | 5 | 209.45 | 23 | 67428 |
| 3 | 1 | 6 | 6 | 303.79 | 20 | 70487 |
| 3 | 1 | 6 | 7 | 184.93 | 16 | 90830 |
| 3 | 1 | 6 | 8 | 62.38 | 2 | 62884 |
| 3 | 1 | 6 | 9 | 6151.48 | 625 | 3050824 |
| 3 | 1 | 7 | 1 | 4918.02 | 236 | 1326307 |
| 3 | 1 | 7 | 2 | 1398.19 | 72 | 342421 |
| 3 | 1 | 7 | 3 | 2349.67 | 45 | 142660 |
| 3 | 1 | 7 | 4 | 252.36 | 15 | 25307 |
| 3 | 1 | 7 | 5 | 881.09 | 52 | 195295 |
| 3 | 1 | 7 | 6 | 1520.51 | 58 | 307753 |
| 3 | 1 | 7 | 7 | 867.16 | 45 | 110181 |
| 3 | 1 | 7 | 8 | 306.00 | 7 | 68657 |
| 3 | 1 | 7 | 9 | 26905.35 | 1481 | 6783057 |
| 3 | 2 | 1 | 1 | 230.25 | 30 | 169977 |
| 3 | 2 | 1 | 2 | 52.01 | 6 | 49480 |
| 3 | 2 | 1 | 3 | 42.02 | 6 | 19600 |
| 3 | 2 | 1 | 4 | 72.26 | 10 | 15713 |
| 3 | 2 | 1 | 5 | 63.55 | 10 | 45597 |
| 3 | 2 | 1 | 6 | 140.48 | 10 | 24925 |
| 3 | 2 | 1 | 7 | 41.12 | 7 | 29069 |
| 3 | 2 | 1 | 8 | 15.44 | 4 | 19159 |
| 3 | 2 | 1 | 9 | 2136.64 | 283 | 1188075 |
| 3 | 2 | 2 | 1 | 304.17 | 33 | 230024 |
| 3 | 2 | 2 | 2 | 74.05 | 9 | 25481 |
| 3 | 2 | 2 | 3 | 44.90 | 3 | 7212 |
| 3 | 2 | 2 | 4 | 74.01 | 1 | 700 |
| 3 | 2 | 2 | 5 | 71.95 | 7 | 12796 |
| 3 | 2 | 2 | 6 | 201.20 | 13 | 30337 |
| 3 | 2 | 2 | 7 | 49.51 | 4 | 35898 |
| 3 | 2 | 2 | 8 | 11.53 | 1 | 5716 |
| 3 | 2 | 2 | 9 | 2535.10 | 241 | 1050750 |
| 3 | 2 | 3 | 1 | 346.82 | 28 | 127469 |
| 3 | 2 | 3 | 2 | 74.87 | 13 | 71451 |
| 3 | 2 | 3 | 3 | 49.48 | 6 | 18584 |
| 3 | 2 | 3 | 4 | 67.62 | 4 | 11510 |
| 3 | 2 | 3 | 5 | 75.80 | 11 | 59922 |
| 3 | 2 | 3 | 6 | 211.42 | 12 | 52349 |
| 3 | 2 | 3 | 7 | 58.59 | 6 | 19142 |
| 3 | 2 | 3 | 8 | 21.15 | 1 | 309 |
| 3 | 2 | 3 | 9 | 2607.48 | 222 | 986926 |
| 3 | 2 | 4 | 1 | 398.70 | 30 | 121008 |
| 3 | 2 | 4 | 2 | 115.52 | 13 | 31036 |
| 3 | 2 | 4 | 3 | 61.44 | 5 | 15124 |
| 3 | 2 | 4 | 4 | 46.99 | 2 | 4809 |
| 3 | 2 | 4 | 5 | 81.79 | 9 | 79729 |
| 3 | 2 | 4 | 6 | 178.98 | 16 | 57389 |
| 3 | 2 | 4 | 7 | 73.74 | 4 | 13266 |
| 3 | 2 | 4 | 8 | 21.73 | 2 | 6506 |
| 3 | 2 | 4 | 9 | 2804.47 | 185 | 983263 |
| 3 | 2 | 5 | 1 | 577.94 | 44 | 164565 |
| 3 | 2 | 5 | 2 | 186.56 | 17 | 37312 |
| 3 | 2 | 5 | 3 | 99.25 | 5 | 70395 |
| 3 | 2 | 5 | 4 | 37.92 | 2 | 3340 |
| 3 | 2 | 5 | 5 | 114.60 | 12 | 36371 |
| 3 | 2 | 5 | 6 | 231.48 | 8 | 12793 |
| 3 | 2 | 5 | 7 | 112.71 | 3 | 7993 |
| 3 | 2 | 5 | 8 | 49.52 | 1 | 7647 |
| 3 | 2 | 5 | 9 | 3785.59 | 255 | 1135808 |
| 3 | 2 | 6 | 1 | 1204.54 | 64 | 297189 |
| 3 | 2 | 6 | 2 | 348.05 | 20 | 87441 |
| 3 | 2 | 6 | 3 | 318.67 | 21 | 132964 |
| 3 | 2 | 6 | 4 | 59.64 | 2 | 2113 |
| 3 | 2 | 6 | 5 | 233.04 | 14 | 55184 |
| 3 | 2 | 6 | 6 | 401.81 | 21 | 79575 |
| 3 | 2 | 6 | 7 | 229.04 | 16 | 63658 |
| 3 | 2 | 6 | 8 | 113.66 | 5 | 69056 |
| 3 | 2 | 6 | 9 | 7232.56 | 477 | 2168736 |
| 3 | 2 | 7 | 1 | 6206.24 | 291 | 1529817 |
| 3 | 2 | 7 | 2 | 1778.53 | 97 | 442424 |
| 3 | 2 | 7 | 3 | 1574.59 | 60 | 408143 |
| 3 | 2 | 7 | 4 | 257.82 | 12 | 34524 |
| 3 | 2 | 7 | 5 | 1214.18 | 67 | 253711 |
| 3 | 2 | 7 | 6 | 1992.86 | 65 | 250177 |
| 3 | 2 | 7 | 7 | 1295.20 | 52 | 296108 |
| 3 | 2 | 7 | 8 | 502.83 | 27 | 92809 |
| 3 | 2 | 7 | 9 | 33844.51 | 1504 | 7698320 |
| 3 | 3 | 1 | 1 | 252.96 | 35 | 165902 |
| 3 | 3 | 1 | 2 | 55.70 | 6 | 15001 |
| 3 | 3 | 1 | 3 | 42.39 | 5 | 19085 |
| 3 | 3 | 1 | 4 | 61.57 | 7 | 47058 |
| 3 | 3 | 1 | 5 | 76.42 | 18 | 103398 |
| 3 | 3 | 1 | 6 | 171.47 | 18 | 101601 |
| 3 | 3 | 1 | 7 | 37.76 | 5 | 7103 |
| 3 | 3 | 1 | 8 | 14.17 | 1 | 31442 |
| 3 | 3 | 1 | 9 | 2164.34 | 294 | 1266124 |
| 3 | 3 | 2 | 1 | 354.49 | 43 | 270211 |
| 3 | 3 | 2 | 2 | 56.21 | 7 | 45695 |
| 3 | 3 | 2 | 3 | 33.16 | 1 | 6939 |
| 3 | 3 | 2 | 4 | 72.74 | 5 | 12904 |
| 3 | 3 | 2 | 5 | 88.73 | 11 | 26769 |
| 3 | 3 | 2 | 6 | 257.15 | 19 | 67830 |
| 3 | 3 | 2 | 7 | 55.78 | 6 | 21727 |
| 3 | 3 | 2 | 8 | 26.57 | 2 | 7009 |
| 3 | 3 | 2 | 9 | 2691.01 | 234 | 1261608 |
| 3 | 3 | 3 | 1 | 388.74 | 25 | 131184 |
| 3 | 3 | 3 | 2 | 71.36 | 7 | 44201 |
| 3 | 3 | 3 | 3 | 38.48 | 1 | 4375 |
| 3 | 3 | 3 | 4 | 71.03 | 2 | 5964 |
| 3 | 3 | 3 | 5 | 86.96 | 11 | 42621 |
| 3 | 3 | 3 | 6 | 250.19 | 20 | 173266 |
| 3 | 3 | 3 | 7 | 75.00 | 6 | 39333 |
| 3 | 3 | 3 | 8 | 34.92 | 5 | 22418 |
| 3 | 3 | 3 | 9 | 2786.03 | 190 | 858717 |
| 3 | 3 | 4 | 1 | 449.50 | 29 | 195168 |
| 3 | 3 | 4 | 2 | 106.66 | 7 | 51072 |
| 3 | 3 | 4 | 3 | 50.85 | 3 | 34954 |
| 3 | 3 | 4 | 4 | 49.51 | 2 | 11339 |
| 3 | 3 | 4 | 5 | 93.52 | 3 | 4737 |
| 3 | 3 | 4 | 6 | 229.73 | 14 | 69250 |
| 3 | 3 | 4 | 7 | 93.86 | 6 | 23703 |
| 3 | 3 | 4 | 8 | 35.25 | 2 | 33142 |
| 3 | 3 | 4 | 9 | 2823.71 | 174 | 804353 |
| 3 | 3 | 5 | 1 | 623.39 | 41 | 164990 |
| 3 | 3 | 5 | 2 | 165.36 | 8 | 49197 |
| 3 | 3 | 5 | 3 | 107.24 | 6 | 9345 |
| 3 | 3 | 5 | 4 | 53.95 | 2 | 4256 |
| 3 | 3 | 5 | 5 | 115.89 | 13 | 33965 |
| 3 | 3 | 5 | 6 | 289.39 | 14 | 64812 |
| 3 | 3 | 5 | 7 | 130.94 | 9 | 58316 |
| 3 | 3 | 5 | 8 | 68.28 | 3 | 5923 |
| 3 | 3 | 5 | 9 | 3795.31 | 233 | 1102967 |
| 3 | 3 | 6 | 1 | 1211.80 | 55 | 204035 |
| 3 | 3 | 6 | 2 | 331.56 | 27 | 160170 |
| 3 | 3 | 6 | 3 | 244.41 | 21 | 112398 |
| 3 | 3 | 6 | 4 | 69.85 | 4 | 7558 |
| 3 | 3 | 6 | 5 | 285.97 | 13 | 72538 |
| 3 | 3 | 6 | 6 | 501.96 | 17 | 79132 |
| 3 | 3 | 6 | 7 | 260.81 | 16 | 66095 |
| 3 | 3 | 6 | 8 | 140.81 | 11 | 99429 |
| 3 | 3 | 6 | 9 | 6982.23 | 418 | 2296256 |
| 3 | 3 | 7 | 1 | 6637.23 | 243 | 1109910 |
| 3 | 3 | 7 | 2 | 1681.52 | 71 | 377529 |
| 3 | 3 | 7 | 3 | 1688.25 | 47 | 211505 |
| 3 | 3 | 7 | 4 | 319.83 | 6 | 49844 |
| 3 | 3 | 7 | 5 | 1402.18 | 55 | 204355 |
| 3 | 3 | 7 | 6 | 2650.35 | 76 | 436313 |
| 3 | 3 | 7 | 7 | 1414.40 | 56 | 314402 |
| 3 | 3 | 7 | 8 | 821.80 | 32 | 244466 |
| 3 | 3 | 7 | 9 | 36595.09 | 1462 | 7765626 |
| 3 | 4 | 1 | 1 | 559.52 | 82 | 333333 |
| 3 | 4 | 1 | 2 | 79.18 | 9 | 83389 |
| 3 | 4 | 1 | 3 | 52.97 | 5 | 10472 |
| 3 | 4 | 1 | 4 | 139.86 | 4 | 13468 |
| 3 | 4 | 1 | 5 | 125.06 | 21 | 139195 |
| 3 | 4 | 1 | 6 | 395.86 | 34 | 101041 |
| 3 | 4 | 1 | 7 | 65.27 | 4 | 13716 |
| 3 | 4 | 1 | 8 | 25.95 | 3 | 14203 |
| 3 | 4 | 1 | 9 | 4174.30 | 477 | 2028574 |
| 3 | 4 | 2 | 1 | 759.38 | 75 | 461748 |
| 3 | 4 | 2 | 2 | 95.99 | 9 | 12058 |
| 3 | 4 | 2 | 3 | 61.91 | 2 | 10300 |
| 3 | 4 | 2 | 4 | 162.43 | 7 | 38966 |
| 3 | 4 | 2 | 5 | 171.40 | 17 | 79870 |
| 3 | 4 | 2 | 6 | 581.13 | 31 | 233888 |
| 3 | 4 | 2 | 7 | 141.70 | 11 | 85892 |
| 3 | 4 | 2 | 8 | 33.05 | 3 | 13031 |
| 3 | 4 | 2 | 9 | 5179.78 | 407 | 2133862 |
| 3 | 4 | 3 | 1 | 882.28 | 67 | 325944 |
| 3 | 4 | 3 | 2 | 140.89 | 6 | 22634 |
| 3 | 4 | 3 | 3 | 80.68 | 1 | 3416 |
| 3 | 4 | 3 | 4 | 120.58 | 3 | 70053 |
| 3 | 4 | 3 | 5 | 168.89 | 12 | 23087 |
| 3 | 4 | 3 | 6 | 566.40 | 24 | 143467 |
| 3 | 4 | 3 | 7 | 141.85 | 13 | 34102 |
| 3 | 4 | 3 | 8 | 59.83 | 5 | 41928 |
| 3 | 4 | 3 | 9 | 5273.39 | 323 | 1769366 |
| 3 | 4 | 4 | 1 | 930.38 | 53 | 294693 |
| 3 | 4 | 4 | 2 | 186.23 | 13 | 91535 |
| 3 | 4 | 4 | 3 | 103.32 | 2 | 12215 |
| 3 | 4 | 4 | 4 | 95.19 | 3 | 36777 |
| 3 | 4 | 4 | 5 | 202.06 | 16 | 71636 |
| 3 | 4 | 4 | 6 | 507.25 | 21 | 47506 |
| 3 | 4 | 4 | 7 | 153.52 | 9 | 81848 |
| 3 | 4 | 4 | 8 | 80.05 | 2 | 7466 |
| 3 | 4 | 4 | 9 | 5361.38 | 290 | 1551046 |
| 3 | 4 | 5 | 1 | 1240.15 | 72 | 441578 |
| 3 | 4 | 5 | 2 | 271.62 | 16 | 87667 |
| 3 | 4 | 5 | 3 | 229.54 | 14 | 83355 |
| 3 | 4 | 5 | 4 | 95.75 | 2 | 8741 |
| 3 | 4 | 5 | 5 | 262.73 | 18 | 44435 |
| 3 | 4 | 5 | 6 | 575.18 | 17 | 65613 |
| 3 | 4 | 5 | 7 | 240.02 | 14 | 28430 |
| 3 | 4 | 5 | 8 | 132.37 | 2 | 7701 |
| 3 | 4 | 5 | 9 | 7316.31 | 332 | 2030248 |
| 3 | 4 | 6 | 1 | 2278.60 | 101 | 444371 |
| 3 | 4 | 6 | 2 | 587.80 | 31 | 122651 |
| 3 | 4 | 6 | 3 | 504.36 | 14 | 103196 |
| 3 | 4 | 6 | 4 | 124.82 | 2 | 31519 |
| 3 | 4 | 6 | 5 | 520.21 | 26 | 116043 |
| 3 | 4 | 6 | 6 | 969.68 | 40 | 193661 |
| 3 | 4 | 6 | 7 | 483.93 | 22 | 64380 |
| 3 | 4 | 6 | 8 | 317.12 | 15 | 150041 |
| 3 | 4 | 6 | 9 | 13375.57 | 616 | 3207923 |
| 3 | 4 | 7 | 1 | 14598.67 | 444 | 2526990 |
| 3 | 4 | 7 | 2 | 3769.94 | 118 | 775364 |
| 3 | 4 | 7 | 3 | 3657.95 | 104 | 731869 |
| 3 | 4 | 7 | 4 | 639.63 | 8 | 13695 |
| 3 | 4 | 7 | 5 | 3018.70 | 95 | 485071 |
| 3 | 4 | 7 | 6 | 6256.55 | 150 | 730785 |
| 3 | 4 | 7 | 7 | 2890.19 | 115 | 676893 |
| 3 | 4 | 7 | 8 | 2160.00 | 55 | 380519 |
| 3 | 4 | 7 | 9 | 79614.96 | 2548 | 13203616 |
| 3 | 5 | 1 | 1 | 66.18 | 11 | 86991 |
| 3 | 5 | 1 | 2 | 12.20 | 2 | 4206 |
| 3 | 5 | 1 | 3 | 10.46 | 0 | 0 |
| 3 | 5 | 1 | 4 | 12.55 | 1 | 31442 |
| 3 | 5 | 1 | 5 | 16.22 | 1 | 617 |
| 3 | 5 | 1 | 6 | 45.16 | 1 | 1606 |
| 3 | 5 | 1 | 7 | 10.26 | 4 | 8787 |
| 3 | 5 | 1 | 8 | 8.14 | 0 | 0 |
| 3 | 5 | 1 | 9 | 582.17 | 82 | 288772 |
| 3 | 5 | 2 | 1 | 95.88 | 4 | 40620 |
| 3 | 5 | 2 | 2 | 14.67 | 1 | 1234 |
| 3 | 5 | 2 | 3 | 9.10 | 0 | 0 |
| 3 | 5 | 2 | 4 | 14.04 | 0 | 0 |
| 3 | 5 | 2 | 5 | 23.38 | 5 | 10834 |
| 3 | 5 | 2 | 6 | 64.73 | 6 | 80041 |
| 3 | 5 | 2 | 7 | 15.78 | 0 | 0 |
| 3 | 5 | 2 | 8 | 7.15 | 0 | 0 |
| 3 | 5 | 2 | 9 | 682.07 | 66 | 251890 |
| 3 | 5 | 3 | 1 | 106.06 | 9 | 52060 |
| 3 | 5 | 3 | 2 | 25.79 | 3 | 5523 |
| 3 | 5 | 3 | 3 | 12.55 | 1 | 901 |
| 3 | 5 | 3 | 4 | 12.61 | 1 | 2693 |
| 3 | 5 | 3 | 5 | 28.41 | 1 | 1300 |
| 3 | 5 | 3 | 6 | 69.25 | 4 | 10121 |
| 3 | 5 | 3 | 7 | 24.06 | 0 | 0 |
| 3 | 5 | 3 | 8 | 7.05 | 0 | 0 |
| 3 | 5 | 3 | 9 | 696.56 | 44 | 270042 |
| 3 | 5 | 4 | 1 | 122.77 | 6 | 40268 |
| 3 | 5 | 4 | 2 | 28.66 | 1 | 1100 |
| 3 | 5 | 4 | 3 | 18.50 | 1 | 1855 |
| 3 | 5 | 4 | 4 | 10.00 | 0 | 0 |
| 3 | 5 | 4 | 5 | 29.15 | 0 | 0 |
| 3 | 5 | 4 | 6 | 71.37 | 4 | 11034 |
| 3 | 5 | 4 | 7 | 22.78 | 1 | 3056 |
| 3 | 5 | 4 | 8 | 10.62 | 2 | 32355 |
| 3 | 5 | 4 | 9 | 741.23 | 44 | 249540 |
| 3 | 5 | 5 | 1 | 186.40 | 6 | 97634 |
| 3 | 5 | 5 | 2 | 39.30 | 2 | 32030 |
| 3 | 5 | 5 | 3 | 31.63 | 2 | 6342 |
| 3 | 5 | 5 | 4 | 5.84 | 0 | 0 |
| 3 | 5 | 5 | 5 | 33.94 | 5 | 13825 |
| 3 | 5 | 5 | 6 | 88.30 | 2 | 32833 |
| 3 | 5 | 5 | 7 | 36.43 | 4 | 3897 |
| 3 | 5 | 5 | 8 | 29.33 | 1 | 31442 |
| 3 | 5 | 5 | 9 | 1017.94 | 56 | 268945 |
| 3 | 5 | 6 | 1 | 359.83 | 15 | 218411 |
| 3 | 5 | 6 | 2 | 79.26 | 10 | 50649 |
| 3 | 5 | 6 | 3 | 73.62 | 5 | 8906 |
| 3 | 5 | 6 | 4 | 13.33 | 0 | 0 |
| 3 | 5 | 6 | 5 | 83.20 | 6 | 49166 |
| 3 | 5 | 6 | 6 | 138.19 | 4 | 18433 |
| 3 | 5 | 6 | 7 | 79.55 | 3 | 12478 |
| 3 | 5 | 6 | 8 | 54.94 | 2 | 4486 |
| 3 | 5 | 6 | 9 | 1941.76 | 89 | 319443 |
| 3 | 5 | 7 | 1 | 1855.30 | 65 | 358790 |
| 3 | 5 | 7 | 2 | 457.25 | 25 | 217118 |
| 3 | 5 | 7 | 3 | 442.87 | 16 | 74000 |
| 3 | 5 | 7 | 4 | 61.12 | 2 | 3887 |
| 3 | 5 | 7 | 5 | 367.21 | 21 | 109371 |
| 3 | 5 | 7 | 6 | 633.37 | 19 | 145079 |
| 3 | 5 | 7 | 7 | 386.49 | 14 | 41905 |
| 3 | 5 | 7 | 8 | 252.47 | 13 | 92133 |
| 3 | 5 | 7 | 9 | 9545.23 | 396 | 1983959 |
| 3 | 6 | 1 | 1 | 187.75 | 35 | 171592 |
| 3 | 6 | 1 | 2 | 24.04 | 4 | 15092 |
| 3 | 6 | 1 | 3 | 13.61 | 2 | 32158 |
| 3 | 6 | 1 | 4 | 33.47 | 1 | 4487 |
| 3 | 6 | 1 | 5 | 41.84 | 8 | 13586 |
| 3 | 6 | 1 | 6 | 136.14 | 19 | 42561 |
| 3 | 6 | 1 | 7 | 30.60 | 1 | 556 |
| 3 | 6 | 1 | 8 | 15.77 | 4 | 4684 |
| 3 | 6 | 1 | 9 | 1238.84 | 140 | 720084 |
| 3 | 6 | 2 | 1 | 259.57 | 30 | 142441 |
| 3 | 6 | 2 | 2 | 29.78 | 1 | 2640 |
| 3 | 6 | 2 | 3 | 16.41 | 0 | 0 |
| 3 | 6 | 2 | 4 | 37.07 | 1 | 9869 |
| 3 | 6 | 2 | 5 | 58.80 | 4 | 11865 |
| 3 | 6 | 2 | 6 | 209.75 | 8 | 80833 |
| 3 | 6 | 2 | 7 | 48.04 | 6 | 17574 |
| 3 | 6 | 2 | 8 | 26.94 | 2 | 9713 |
| 3 | 6 | 2 | 9 | 1626.78 | 125 | 470051 |
| 3 | 6 | 3 | 1 | 299.91 | 19 | 169849 |
| 3 | 6 | 3 | 2 | 28.45 | 0 | 0 |
| 3 | 6 | 3 | 3 | 22.83 | 0 | 0 |
| 3 | 6 | 3 | 4 | 30.88 | 0 | 0 |
| 3 | 6 | 3 | 5 | 54.01 | 4 | 4943 |
| 3 | 6 | 3 | 6 | 181.06 | 11 | 42891 |
| 3 | 6 | 3 | 7 | 46.17 | 0 | 0 |
| 3 | 6 | 3 | 8 | 38.09 | 3 | 3450 |
| 3 | 6 | 3 | 9 | 1632.96 | 92 | 403488 |
| 3 | 6 | 4 | 1 | 300.59 | 17 | 117401 |
| 3 | 6 | 4 | 2 | 44.31 | 5 | 12173 |
| 3 | 6 | 4 | 3 | 28.00 | 0 | 0 |
| 3 | 6 | 4 | 4 | 19.33 | 0 | 0 |
| 3 | 6 | 4 | 5 | 53.55 | 3 | 5949 |
| 3 | 6 | 4 | 6 | 163.02 | 7 | 25358 |
| 3 | 6 | 4 | 7 | 58.78 | 5 | 43236 |
| 3 | 6 | 4 | 8 | 46.23 | 2 | 1803 |
| 3 | 6 | 4 | 9 | 1577.85 | 80 | 447128 |
| 3 | 6 | 5 | 1 | 385.54 | 16 | 110578 |
| 3 | 6 | 5 | 2 | 84.29 | 6 | 13624 |
| 3 | 6 | 5 | 3 | 64.25 | 1 | 1518 |
| 3 | 6 | 5 | 4 | 23.74 | 0 | 0 |
| 3 | 6 | 5 | 5 | 78.56 | 6 | 20737 |
| 3 | 6 | 5 | 6 | 198.91 | 7 | 20881 |
| 3 | 6 | 5 | 7 | 68.71 | 2 | 9151 |
| 3 | 6 | 5 | 8 | 61.13 | 3 | 18101 |
| 3 | 6 | 5 | 9 | 2017.86 | 112 | 644496 |
| 3 | 6 | 6 | 1 | 772.69 | 32 | 120917 |
| 3 | 6 | 6 | 2 | 188.97 | 11 | 69871 |
| 3 | 6 | 6 | 3 | 141.34 | 4 | 49093 |
| 3 | 6 | 6 | 4 | 35.49 | 0 | 0 |
| 3 | 6 | 6 | 5 | 160.82 | 7 | 53193 |
| 3 | 6 | 6 | 6 | 328.78 | 17 | 79488 |
| 3 | 6 | 6 | 7 | 136.87 | 11 | 36441 |
| 3 | 6 | 6 | 8 | 155.63 | 4 | 35412 |
| 3 | 6 | 6 | 9 | 3855.71 | 164 | 981465 |
| 3 | 6 | 7 | 1 | 4739.07 | 156 | 1031429 |
| 3 | 6 | 7 | 2 | 1134.37 | 45 | 235652 |
| 3 | 6 | 7 | 3 | 1078.25 | 32 | 168555 |
| 3 | 6 | 7 | 4 | 151.43 | 2 | 5982 |
| 3 | 6 | 7 | 5 | 971.01 | 35 | 95823 |
| 3 | 6 | 7 | 6 | 1928.14 | 45 | 368238 |
| 3 | 6 | 7 | 7 | 889.08 | 27 | 89649 |
| 3 | 6 | 7 | 8 | 900.56 | 35 | 228604 |
| 3 | 6 | 7 | 9 | 22985.48 | 799 | 4265828 |
| 3 | 7 | 1 | 1 | 3.39 | 1 | 303 |
| 3 | 7 | 1 | 2 | 2.34 | 0 | 0 |
| 3 | 7 | 1 | 3 | 0.80 | 0 | 0 |
| 3 | 7 | 1 | 4 | 2.49 | 0 | 0 |
| 3 | 7 | 1 | 5 | 1.34 | 1 | 906 |
| 3 | 7 | 1 | 6 | 8.71 | 0 | 0 |
| 3 | 7 | 1 | 7 | 1.63 | 0 | 0 |
| 3 | 7 | 1 | 8 | 0.15 | 0 | 0 |
| 3 | 7 | 1 | 9 | 78.57 | 6 | 66711 |
| 3 | 7 | 2 | 1 | 19.19 | 0 | 0 |
| 3 | 7 | 2 | 2 | 3.27 | 0 | 0 |
| 3 | 7 | 2 | 3 | 0.38 | 0 | 0 |
| 3 | 7 | 2 | 4 | 5.71 | 1 | 31442 |
| 3 | 7 | 2 | 5 | 4.12 | 1 | 31442 |
| 3 | 7 | 2 | 6 | 10.07 | 0 | 0 |
| 3 | 7 | 2 | 7 | 3.24 | 0 | 0 |
| 3 | 7 | 2 | 8 | 1.28 | 0 | 0 |
| 3 | 7 | 2 | 9 | 111.66 | 10 | 33310 |
| 3 | 7 | 3 | 1 | 15.14 | 1 | 1441 |
| 3 | 7 | 3 | 2 | 4.09 | 0 | 0 |
| 3 | 7 | 3 | 3 | 0.90 | 0 | 0 |
| 3 | 7 | 3 | 4 | 1.06 | 0 | 0 |
| 3 | 7 | 3 | 5 | 2.02 | 0 | 0 |
| 3 | 7 | 3 | 6 | 6.70 | 0 | 0 |
| 3 | 7 | 3 | 7 | 1.00 | 0 | 0 |
| 3 | 7 | 3 | 8 | 0.76 | 0 | 0 |
| 3 | 7 | 3 | 9 | 105.76 | 8 | 14449 |
| 3 | 7 | 4 | 1 | 14.41 | 0 | 0 |
| 3 | 7 | 4 | 2 | 1.92 | 1 | 794 |
| 3 | 7 | 4 | 3 | 0.96 | 0 | 0 |
| 3 | 7 | 4 | 4 | 1.16 | 0 | 0 |
| 3 | 7 | 4 | 5 | 3.85 | 0 | 0 |
| 3 | 7 | 4 | 6 | 5.92 | 0 | 0 |
| 3 | 7 | 4 | 7 | 1.90 | 3 | 11762 |
| 3 | 7 | 4 | 8 | 2.21 | 0 | 0 |
| 3 | 7 | 4 | 9 | 110.85 | 5 | 41333 |
| 3 | 7 | 5 | 1 | 14.35 | 0 | 0 |
| 3 | 7 | 5 | 2 | 4.57 | 0 | 0 |
| 3 | 7 | 5 | 3 | 3.34 | 0 | 0 |
| 3 | 7 | 5 | 4 | 3.56 | 0 | 0 |
| 3 | 7 | 5 | 5 | 7.44 | 0 | 0 |
| 3 | 7 | 5 | 6 | 13.81 | 0 | 0 |
| 3 | 7 | 5 | 7 | 4.92 | 0 | 0 |
| 3 | 7 | 5 | 8 | 1.16 | 0 | 0 |
| 3 | 7 | 5 | 9 | 146.21 | 7 | 49986 |
| 3 | 7 | 6 | 1 | 31.22 | 2 | 4738 |
| 3 | 7 | 6 | 2 | 14.40 | 0 | 0 |
| 3 | 7 | 6 | 3 | 4.81 | 0 | 0 |
| 3 | 7 | 6 | 4 | 6.03 | 0 | 0 |
| 3 | 7 | 6 | 5 | 4.25 | 2 | 2063 |
| 3 | 7 | 6 | 6 | 13.08 | 1 | 1769 |
| 3 | 7 | 6 | 7 | 10.27 | 0 | 0 |
| 3 | 7 | 6 | 8 | 6.33 | 0 | 0 |
| 3 | 7 | 6 | 9 | 292.33 | 10 | 22382 |
| 3 | 7 | 7 | 1 | 288.36 | 12 | 41206 |
| 3 | 7 | 7 | 2 | 84.68 | 1 | 1200 |
| 3 | 7 | 7 | 3 | 29.99 | 1 | 31442 |
| 3 | 7 | 7 | 4 | 19.07 | 1 | 3608 |
| 3 | 7 | 7 | 5 | 37.96 | 1 | 1455 |
| 3 | 7 | 7 | 6 | 113.33 | 2 | 7618 |
| 3 | 7 | 7 | 7 | 40.84 | 2 | 34979 |
| 3 | 7 | 7 | 8 | 34.87 | 0 | 0 |
| 3 | 7 | 7 | 9 | 1720.36 | 57 | 226934 |
| 4 | 1 | 1 | 1 | 49.31 | 11 | 23218 |
| 4 | 1 | 1 | 2 | 22.93 | 6 | 14940 |
| 4 | 1 | 1 | 3 | 34.01 | 9 | 101091 |
| 4 | 1 | 1 | 4 | 6.08 | 0 | 0 |
| 4 | 1 | 1 | 5 | 17.77 | 4 | 4164 |
| 4 | 1 | 1 | 6 | 18.59 | 1 | 3044 |
| 4 | 1 | 1 | 7 | 3.89 | 0 | 0 |
| 4 | 1 | 1 | 8 | 4.31 | 1 | 400 |
| 4 | 1 | 1 | 9 | 601.75 | 103 | 381138 |
| 4 | 1 | 2 | 1 | 77.53 | 6 | 16812 |
| 4 | 1 | 2 | 2 | 29.09 | 5 | 9656 |
| 4 | 1 | 2 | 3 | 36.39 | 6 | 10543 |
| 4 | 1 | 2 | 4 | 11.32 | 1 | 8231 |
| 4 | 1 | 2 | 5 | 18.74 | 3 | 4571 |
| 4 | 1 | 2 | 6 | 32.02 | 3 | 38542 |
| 4 | 1 | 2 | 7 | 13.62 | 1 | 954 |
| 4 | 1 | 2 | 8 | 3.73 | 0 | 0 |
| 4 | 1 | 2 | 9 | 735.71 | 86 | 391512 |
| 4 | 1 | 3 | 1 | 85.77 | 4 | 14451 |
| 4 | 1 | 3 | 2 | 36.08 | 2 | 3784 |
| 4 | 1 | 3 | 3 | 34.31 | 6 | 8274 |
| 4 | 1 | 3 | 4 | 12.01 | 1 | 917 |
| 4 | 1 | 3 | 5 | 19.10 | 4 | 14439 |
| 4 | 1 | 3 | 6 | 32.80 | 4 | 12608 |
| 4 | 1 | 3 | 7 | 18.59 | 1 | 900 |
| 4 | 1 | 3 | 8 | 8.54 | 3 | 4956 |
| 4 | 1 | 3 | 9 | 729.62 | 88 | 599538 |
| 4 | 1 | 4 | 1 | 105.73 | 15 | 90111 |
| 4 | 1 | 4 | 2 | 35.14 | 6 | 38663 |
| 4 | 1 | 4 | 3 | 53.38 | 1 | 3000 |
| 4 | 1 | 4 | 4 | 6.89 | 1 | 4686 |
| 4 | 1 | 4 | 5 | 18.19 | 3 | 3372 |
| 4 | 1 | 4 | 6 | 34.63 | 2 | 3178 |
| 4 | 1 | 4 | 7 | 16.77 | 0 | 0 |
| 4 | 1 | 4 | 8 | 11.75 | 0 | 0 |
| 4 | 1 | 4 | 9 | 766.14 | 71 | 430373 |
| 4 | 1 | 5 | 1 | 166.10 | 7 | 40729 |
| 4 | 1 | 5 | 2 | 66.54 | 5 | 43356 |
| 4 | 1 | 5 | 3 | 48.99 | 7 | 17562 |
| 4 | 1 | 5 | 4 | 10.91 | 1 | 993 |
| 4 | 1 | 5 | 5 | 32.50 | 5 | 47591 |
| 4 | 1 | 5 | 6 | 53.90 | 4 | 15205 |
| 4 | 1 | 5 | 7 | 17.88 | 2 | 8643 |
| 4 | 1 | 5 | 8 | 17.04 | 2 | 3314 |
| 4 | 1 | 5 | 9 | 1064.66 | 96 | 403899 |
| 4 | 1 | 6 | 1 | 344.68 | 32 | 184118 |
| 4 | 1 | 6 | 2 | 125.36 | 15 | 34894 |
| 4 | 1 | 6 | 3 | 130.03 | 11 | 66353 |
| 4 | 1 | 6 | 4 | 15.00 | 0 | 0 |
| 4 | 1 | 6 | 5 | 73.29 | 10 | 122551 |
| 4 | 1 | 6 | 6 | 95.16 | 4 | 9655 |
| 4 | 1 | 6 | 7 | 51.85 | 3 | 33098 |
| 4 | 1 | 6 | 8 | 35.32 | 5 | 12104 |
| 4 | 1 | 6 | 9 | 2154.39 | 173 | 702215 |
| 4 | 1 | 7 | 1 | 1528.57 | 87 | 483084 |
| 4 | 1 | 7 | 2 | 567.56 | 35 | 209646 |
| 4 | 1 | 7 | 3 | 563.23 | 34 | 107767 |
| 4 | 1 | 7 | 4 | 65.95 | 3 | 12950 |
| 4 | 1 | 7 | 5 | 278.46 | 24 | 93032 |
| 4 | 1 | 7 | 6 | 395.47 | 10 | 27088 |
| 4 | 1 | 7 | 7 | 230.90 | 5 | 22495 |
| 4 | 1 | 7 | 8 | 163.53 | 8 | 27401 |
| 4 | 1 | 7 | 9 | 8738.13 | 520 | 2437429 |
| 4 | 2 | 1 | 1 | 52.42 | 9 | 50023 |
| 4 | 2 | 1 | 2 | 18.13 | 3 | 33786 |
| 4 | 2 | 1 | 3 | 13.45 | 0 | 0 |
| 4 | 2 | 1 | 4 | 7.31 | 2 | 6906 |
| 4 | 2 | 1 | 5 | 17.93 | 7 | 18501 |
| 4 | 2 | 1 | 6 | 35.36 | 2 | 5317 |
| 4 | 2 | 1 | 7 | 10.18 | 2 | 1329 |
| 4 | 2 | 1 | 8 | 3.66 | 2 | 3465 |
| 4 | 2 | 1 | 9 | 510.14 | 83 | 357640 |
| 4 | 2 | 2 | 1 | 73.64 | 7 | 45054 |
| 4 | 2 | 2 | 2 | 25.83 | 4 | 12796 |
| 4 | 2 | 2 | 3 | 17.27 | 1 | 148 |
| 4 | 2 | 2 | 4 | 14.44 | 0 | 0 |
| 4 | 2 | 2 | 5 | 23.46 | 2 | 6103 |
| 4 | 2 | 2 | 6 | 58.09 | 5 | 36882 |
| 4 | 2 | 2 | 7 | 20.45 | 2 | 4383 |
| 4 | 2 | 2 | 8 | 6.65 | 0 | 0 |
| 4 | 2 | 2 | 9 | 720.52 | 98 | 456585 |
| 4 | 2 | 3 | 1 | 126.64 | 11 | 28994 |
| 4 | 2 | 3 | 2 | 35.86 | 4 | 8066 |
| 4 | 2 | 3 | 3 | 21.01 | 2 | 10160 |
| 4 | 2 | 3 | 4 | 16.24 | 0 | 0 |
| 4 | 2 | 3 | 5 | 19.53 | 1 | 6861 |
| 4 | 2 | 3 | 6 | 56.42 | 3 | 7874 |
| 4 | 2 | 3 | 7 | 26.02 | 3 | 10624 |
| 4 | 2 | 3 | 8 | 10.09 | 2 | 6237 |
| 4 | 2 | 3 | 9 | 855.76 | 62 | 303872 |
| 4 | 2 | 4 | 1 | 138.08 | 16 | 134301 |
| 4 | 2 | 4 | 2 | 41.49 | 3 | 7068 |
| 4 | 2 | 4 | 3 | 34.65 | 3 | 38011 |
| 4 | 2 | 4 | 4 | 12.24 | 0 | 0 |
| 4 | 2 | 4 | 5 | 24.21 | 6 | 25737 |
| 4 | 2 | 4 | 6 | 54.79 | 2 | 2560 |
| 4 | 2 | 4 | 7 | 34.39 | 2 | 34833 |
| 4 | 2 | 4 | 8 | 12.31 | 0 | 0 |
| 4 | 2 | 4 | 9 | 903.99 | 70 | 360223 |
| 4 | 2 | 5 | 1 | 199.99 | 14 | 66020 |
| 4 | 2 | 5 | 2 | 67.63 | 8 | 23998 |
| 4 | 2 | 5 | 3 | 44.13 | 1 | 2288 |
| 4 | 2 | 5 | 4 | 12.04 | 0 | 0 |
| 4 | 2 | 5 | 5 | 37.01 | 2 | 5688 |
| 4 | 2 | 5 | 6 | 67.39 | 4 | 5756 |
| 4 | 2 | 5 | 7 | 38.42 | 3 | 4812 |
| 4 | 2 | 5 | 8 | 20.27 | 4 | 36477 |
| 4 | 2 | 5 | 9 | 1305.83 | 99 | 321088 |
| 4 | 2 | 6 | 1 | 452.94 | 31 | 97902 |
| 4 | 2 | 6 | 2 | 166.21 | 17 | 158030 |
| 4 | 2 | 6 | 3 | 127.04 | 10 | 66279 |
| 4 | 2 | 6 | 4 | 16.52 | 1 | 1800 |
| 4 | 2 | 6 | 5 | 91.55 | 8 | 9753 |
| 4 | 2 | 6 | 6 | 135.02 | 3 | 8171 |
| 4 | 2 | 6 | 7 | 83.37 | 7 | 14223 |
| 4 | 2 | 6 | 8 | 65.80 | 1 | 4332 |
| 4 | 2 | 6 | 9 | 2702.27 | 157 | 912421 |
| 4 | 2 | 7 | 1 | 2110.59 | 107 | 595146 |
| 4 | 2 | 7 | 2 | 708.77 | 43 | 155553 |
| 4 | 2 | 7 | 3 | 717.74 | 28 | 222823 |
| 4 | 2 | 7 | 4 | 55.84 | 2 | 5417 |
| 4 | 2 | 7 | 5 | 403.75 | 21 | 52327 |
| 4 | 2 | 7 | 6 | 630.80 | 30 | 78258 |
| 4 | 2 | 7 | 7 | 410.91 | 26 | 73043 |
| 4 | 2 | 7 | 8 | 328.26 | 5 | 14963 |
| 4 | 2 | 7 | 9 | 12169.67 | 598 | 3223609 |
| 4 | 3 | 1 | 1 | 70.13 | 12 | 55595 |
| 4 | 3 | 1 | 2 | 17.58 | 1 | 8064 |
| 4 | 3 | 1 | 3 | 23.46 | 2 | 6214 |
| 4 | 3 | 1 | 4 | 11.23 | 1 | 8670 |
| 4 | 3 | 1 | 5 | 13.24 | 3 | 2138 |
| 4 | 3 | 1 | 6 | 47.61 | 5 | 12105 |
| 4 | 3 | 1 | 7 | 11.87 | 0 | 0 |
| 4 | 3 | 1 | 8 | 5.77 | 0 | 0 |
| 4 | 3 | 1 | 9 | 499.28 | 52 | 237894 |
| 4 | 3 | 2 | 1 | 112.86 | 11 | 25656 |
| 4 | 3 | 2 | 2 | 26.77 | 1 | 3915 |
| 4 | 3 | 2 | 3 | 25.69 | 7 | 41229 |
| 4 | 3 | 2 | 4 | 11.26 | 1 | 3468 |
| 4 | 3 | 2 | 5 | 23.55 | 3 | 2732 |
| 4 | 3 | 2 | 6 | 78.70 | 6 | 18099 |
| 4 | 3 | 2 | 7 | 19.31 | 4 | 8908 |
| 4 | 3 | 2 | 8 | 7.38 | 1 | 31442 |
| 4 | 3 | 2 | 9 | 784.88 | 74 | 291386 |
| 4 | 3 | 3 | 1 | 132.22 | 11 | 112977 |
| 4 | 3 | 3 | 2 | 32.33 | 2 | 5747 |
| 4 | 3 | 3 | 3 | 23.84 | 1 | 31442 |
| 4 | 3 | 3 | 4 | 12.19 | 1 | 2400 |
| 4 | 3 | 3 | 5 | 31.33 | 1 | 939 |
| 4 | 3 | 3 | 6 | 92.30 | 6 | 47618 |
| 4 | 3 | 3 | 7 | 18.55 | 3 | 10335 |
| 4 | 3 | 3 | 8 | 7.26 | 0 | 0 |
| 4 | 3 | 3 | 9 | 881.54 | 46 | 198404 |
| 4 | 3 | 4 | 1 | 181.06 | 9 | 45410 |
| 4 | 3 | 4 | 2 | 46.47 | 0 | 0 |
| 4 | 3 | 4 | 3 | 29.81 | 0 | 0 |
| 4 | 3 | 4 | 4 | 9.02 | 0 | 0 |
| 4 | 3 | 4 | 5 | 31.21 | 6 | 44195 |
| 4 | 3 | 4 | 6 | 89.92 | 3 | 10382 |
| 4 | 3 | 4 | 7 | 31.18 | 2 | 3523 |
| 4 | 3 | 4 | 8 | 17.15 | 3 | 10519 |
| 4 | 3 | 4 | 9 | 958.53 | 73 | 380081 |
| 4 | 3 | 5 | 1 | 232.21 | 9 | 86821 |
| 4 | 3 | 5 | 2 | 55.68 | 0 | 0 |
| 4 | 3 | 5 | 3 | 48.14 | 2 | 34624 |
| 4 | 3 | 5 | 4 | 12.63 | 0 | 0 |
| 4 | 3 | 5 | 5 | 52.17 | 2 | 3952 |
| 4 | 3 | 5 | 6 | 107.44 | 6 | 46145 |
| 4 | 3 | 5 | 7 | 40.18 | 5 | 11704 |
| 4 | 3 | 5 | 8 | 38.26 | 0 | 0 |
| 4 | 3 | 5 | 9 | 1404.67 | 95 | 417261 |
| 4 | 3 | 6 | 1 | 502.26 | 23 | 107693 |
| 4 | 3 | 6 | 2 | 135.72 | 14 | 84314 |
| 4 | 3 | 6 | 3 | 140.08 | 5 | 9624 |
| 4 | 3 | 6 | 4 | 17.48 | 0 | 0 |
| 4 | 3 | 6 | 5 | 107.97 | 5 | 17978 |
| 4 | 3 | 6 | 6 | 143.88 | 11 | 27311 |
| 4 | 3 | 6 | 7 | 87.39 | 8 | 42469 |
| 4 | 3 | 6 | 8 | 82.11 | 4 | 18826 |
| 4 | 3 | 6 | 9 | 2805.94 | 139 | 733705 |
| 4 | 3 | 7 | 1 | 2312.76 | 107 | 695827 |
| 4 | 3 | 7 | 2 | 676.83 | 29 | 146054 |
| 4 | 3 | 7 | 3 | 748.35 | 33 | 169849 |
| 4 | 3 | 7 | 4 | 79.77 | 5 | 42430 |
| 4 | 3 | 7 | 5 | 504.39 | 18 | 66503 |
| 4 | 3 | 7 | 6 | 862.65 | 25 | 124101 |
| 4 | 3 | 7 | 7 | 512.76 | 17 | 59311 |
| 4 | 3 | 7 | 8 | 470.40 | 22 | 121196 |
| 4 | 3 | 7 | 9 | 13951.57 | 584 | 2899470 |
| 4 | 4 | 1 | 1 | 172.47 | 21 | 105510 |
| 4 | 4 | 1 | 2 | 26.09 | 0 | 0 |
| 4 | 4 | 1 | 3 | 30.77 | 5 | 40261 |
| 4 | 4 | 1 | 4 | 13.54 | 0 | 0 |
| 4 | 4 | 1 | 5 | 30.82 | 3 | 43190 |
| 4 | 4 | 1 | 6 | 104.04 | 9 | 25652 |
| 4 | 4 | 1 | 7 | 20.72 | 4 | 7244 |
| 4 | 4 | 1 | 8 | 11.16 | 2 | 2280 |
| 4 | 4 | 1 | 9 | 944.79 | 90 | 407441 |
| 4 | 4 | 2 | 1 | 269.84 | 31 | 271937 |
| 4 | 4 | 2 | 2 | 44.88 | 4 | 18343 |
| 4 | 4 | 2 | 3 | 43.45 | 4 | 16229 |
| 4 | 4 | 2 | 4 | 35.07 | 2 | 1770 |
| 4 | 4 | 2 | 5 | 48.57 | 7 | 18027 |
| 4 | 4 | 2 | 6 | 164.27 | 13 | 55542 |
| 4 | 4 | 2 | 7 | 31.44 | 2 | 2738 |
| 4 | 4 | 2 | 8 | 21.80 | 2 | 1710 |
| 4 | 4 | 2 | 9 | 1582.15 | 144 | 690199 |
| 4 | 4 | 3 | 1 | 324.35 | 21 | 81074 |
| 4 | 4 | 3 | 2 | 67.35 | 5 | 7762 |
| 4 | 4 | 3 | 3 | 35.51 | 2 | 2184 |
| 4 | 4 | 3 | 4 | 17.58 | 1 | 1500 |
| 4 | 4 | 3 | 5 | 49.59 | 6 | 12520 |
| 4 | 4 | 3 | 6 | 164.43 | 15 | 139115 |
| 4 | 4 | 3 | 7 | 48.55 | 5 | 9487 |
| 4 | 4 | 3 | 8 | 28.33 | 2 | 34108 |
| 4 | 4 | 3 | 9 | 1687.61 | 120 | 623928 |
| 4 | 4 | 4 | 1 | 328.35 | 21 | 88706 |
| 4 | 4 | 4 | 2 | 80.47 | 5 | 6326 |
| 4 | 4 | 4 | 3 | 56.09 | 3 | 5281 |
| 4 | 4 | 4 | 4 | 20.88 | 0 | 0 |
| 4 | 4 | 4 | 5 | 64.24 | 4 | 39255 |
| 4 | 4 | 4 | 6 | 174.10 | 9 | 57665 |
| 4 | 4 | 4 | 7 | 50.19 | 3 | 7652 |
| 4 | 4 | 4 | 8 | 55.60 | 4 | 9368 |
| 4 | 4 | 4 | 9 | 1907.97 | 101 | 489424 |
| 4 | 4 | 5 | 1 | 481.30 | 30 | 86157 |
| 4 | 4 | 5 | 2 | 130.83 | 4 | 41552 |
| 4 | 4 | 5 | 3 | 93.20 | 4 | 45751 |
| 4 | 4 | 5 | 4 | 21.78 | 1 | 2193 |
| 4 | 4 | 5 | 5 | 83.41 | 8 | 27643 |
| 4 | 4 | 5 | 6 | 228.49 | 12 | 113934 |
| 4 | 4 | 5 | 7 | 90.12 | 5 | 14731 |
| 4 | 4 | 5 | 8 | 84.36 | 7 | 13308 |
| 4 | 4 | 5 | 9 | 2775.52 | 160 | 865925 |
| 4 | 4 | 6 | 1 | 978.57 | 44 | 304384 |
| 4 | 4 | 6 | 2 | 284.51 | 12 | 110861 |
| 4 | 4 | 6 | 3 | 259.23 | 15 | 36007 |
| 4 | 4 | 6 | 4 | 36.88 | 0 | 0 |
| 4 | 4 | 6 | 5 | 179.94 | 6 | 57514 |
| 4 | 4 | 6 | 6 | 398.99 | 18 | 123132 |
| 4 | 4 | 6 | 7 | 159.68 | 7 | 42550 |
| 4 | 4 | 6 | 8 | 179.44 | 15 | 135172 |
| 4 | 4 | 6 | 9 | 5553.54 | 255 | 1529493 |
| 4 | 4 | 7 | 1 | 5091.56 | 187 | 1200157 |
| 4 | 4 | 7 | 2 | 1618.34 | 67 | 364718 |
| 4 | 4 | 7 | 3 | 1710.88 | 74 | 348802 |
| 4 | 4 | 7 | 4 | 166.09 | 4 | 7563 |
| 4 | 4 | 7 | 5 | 1098.94 | 50 | 223397 |
| 4 | 4 | 7 | 6 | 2288.50 | 62 | 240148 |
| 4 | 4 | 7 | 7 | 1101.12 | 46 | 264633 |
| 4 | 4 | 7 | 8 | 1289.41 | 43 | 195629 |
| 4 | 4 | 7 | 9 | 30873.62 | 1186 | 6834531 |
| 4 | 5 | 1 | 1 | 14.14 | 2 | 2676 |
| 4 | 5 | 1 | 2 | 3.98 | 2 | 9979 |
| 4 | 5 | 1 | 3 | 1.93 | 0 | 0 |
| 4 | 5 | 1 | 4 | 0.13 | 0 | 0 |
| 4 | 5 | 1 | 5 | 5.26 | 1 | 600 |
| 4 | 5 | 1 | 6 | 12.36 | 2 | 7638 |
| 4 | 5 | 1 | 7 | 1.14 | 0 | 0 |
| 4 | 5 | 1 | 8 | 1.02 | 0 | 0 |
| 4 | 5 | 1 | 9 | 110.40 | 14 | 61788 |
| 4 | 5 | 2 | 1 | 22.43 | 1 | 1825 |
| 4 | 5 | 2 | 2 | 6.47 | 0 | 0 |
| 4 | 5 | 2 | 3 | 3.74 | 0 | 0 |
| 4 | 5 | 2 | 4 | 3.60 | 0 | 0 |
| 4 | 5 | 2 | 5 | 4.65 | 0 | 0 |
| 4 | 5 | 2 | 6 | 19.16 | 1 | 1258 |
| 4 | 5 | 2 | 7 | 3.64 | 1 | 72 |
| 4 | 5 | 2 | 8 | 2.05 | 0 | 0 |
| 4 | 5 | 2 | 9 | 184.50 | 17 | 134556 |
| 4 | 5 | 3 | 1 | 28.65 | 3 | 2343 |
| 4 | 5 | 3 | 2 | 10.98 | 1 | 5762 |
| 4 | 5 | 3 | 3 | 5.65 | 0 | 0 |
| 4 | 5 | 3 | 4 | 2.86 | 0 | 0 |
| 4 | 5 | 3 | 5 | 6.91 | 1 | 956 |
| 4 | 5 | 3 | 6 | 26.36 | 2 | 11007 |
| 4 | 5 | 3 | 7 | 3.84 | 1 | 2330 |
| 4 | 5 | 3 | 8 | 1.86 | 0 | 0 |
| 4 | 5 | 3 | 9 | 210.68 | 12 | 49731 |
| 4 | 5 | 4 | 1 | 41.28 | 1 | 4333 |
| 4 | 5 | 4 | 2 | 9.24 | 1 | 31442 |
| 4 | 5 | 4 | 3 | 9.24 | 1 | 1684 |
| 4 | 5 | 4 | 4 | 2.81 | 0 | 0 |
| 4 | 5 | 4 | 5 | 8.87 | 0 | 0 |
| 4 | 5 | 4 | 6 | 20.82 | 1 | 5368 |
| 4 | 5 | 4 | 7 | 8.46 | 0 | 0 |
| 4 | 5 | 4 | 8 | 4.40 | 0 | 0 |
| 4 | 5 | 4 | 9 | 235.24 | 15 | 106855 |
| 4 | 5 | 5 | 1 | 59.64 | 5 | 18003 |
| 4 | 5 | 5 | 2 | 13.54 | 0 | 0 |
| 4 | 5 | 5 | 3 | 9.66 | 1 | 31442 |
| 4 | 5 | 5 | 4 | 0.75 | 0 | 0 |
| 4 | 5 | 5 | 5 | 12.18 | 0 | 0 |
| 4 | 5 | 5 | 6 | 25.69 | 0 | 0 |
| 4 | 5 | 5 | 7 | 14.53 | 0 | 0 |
| 4 | 5 | 5 | 8 | 9.86 | 0 | 0 |
| 4 | 5 | 5 | 9 | 348.30 | 30 | 250211 |
| 4 | 5 | 6 | 1 | 136.90 | 12 | 96970 |
| 4 | 5 | 6 | 2 | 30.74 | 1 | 1503 |
| 4 | 5 | 6 | 3 | 38.50 | 3 | 35613 |
| 4 | 5 | 6 | 4 | 2.31 | 0 | 0 |
| 4 | 5 | 6 | 5 | 31.50 | 3 | 6302 |
| 4 | 5 | 6 | 6 | 39.79 | 3 | 34383 |
| 4 | 5 | 6 | 7 | 27.33 | 1 | 31442 |
| 4 | 5 | 6 | 8 | 26.32 | 2 | 34167 |
| 4 | 5 | 6 | 9 | 755.36 | 47 | 255811 |
| 4 | 5 | 7 | 1 | 593.04 | 21 | 123958 |
| 4 | 5 | 7 | 2 | 158.87 | 11 | 47492 |
| 4 | 5 | 7 | 3 | 196.15 | 9 | 30277 |
| 4 | 5 | 7 | 4 | 12.98 | 0 | 0 |
| 4 | 5 | 7 | 5 | 104.85 | 1 | 1978 |
| 4 | 5 | 7 | 6 | 194.90 | 4 | 10588 |
| 4 | 5 | 7 | 7 | 138.42 | 7 | 67566 |
| 4 | 5 | 7 | 8 | 149.13 | 3 | 9709 |
| 4 | 5 | 7 | 9 | 3152.35 | 156 | 768061 |
| 4 | 6 | 1 | 1 | 59.95 | 10 | 31740 |
| 4 | 6 | 1 | 2 | 8.18 | 0 | 0 |
| 4 | 6 | 1 | 3 | 7.13 | 1 | 2360 |
| 4 | 6 | 1 | 4 | 2.32 | 0 | 0 |
| 4 | 6 | 1 | 5 | 8.74 | 2 | 13931 |
| 4 | 6 | 1 | 6 | 25.54 | 3 | 32660 |
| 4 | 6 | 1 | 7 | 7.17 | 2 | 4415 |
| 4 | 6 | 1 | 8 | 3.47 | 0 | 0 |
| 4 | 6 | 1 | 9 | 282.66 | 22 | 56172 |
| 4 | 6 | 2 | 1 | 93.52 | 11 | 25417 |
| 4 | 6 | 2 | 2 | 7.56 | 0 | 0 |
| 4 | 6 | 2 | 3 | 5.70 | 0 | 0 |
| 4 | 6 | 2 | 4 | 3.57 | 0 | 0 |
| 4 | 6 | 2 | 5 | 11.91 | 3 | 41995 |
| 4 | 6 | 2 | 6 | 70.70 | 3 | 11924 |
| 4 | 6 | 2 | 7 | 10.96 | 1 | 31442 |
| 4 | 6 | 2 | 8 | 9.96 | 0 | 0 |
| 4 | 6 | 2 | 9 | 468.91 | 34 | 209378 |
| 4 | 6 | 3 | 1 | 104.27 | 8 | 51392 |
| 4 | 6 | 3 | 2 | 16.00 | 1 | 1363 |
| 4 | 6 | 3 | 3 | 9.16 | 2 | 4211 |
| 4 | 6 | 3 | 4 | 5.50 | 0 | 0 |
| 4 | 6 | 3 | 5 | 11.33 | 1 | 3759 |
| 4 | 6 | 3 | 6 | 58.02 | 3 | 10592 |
| 4 | 6 | 3 | 7 | 19.89 | 2 | 8013 |
| 4 | 6 | 3 | 8 | 11.80 | 1 | 6140 |
| 4 | 6 | 3 | 9 | 517.45 | 34 | 165960 |
| 4 | 6 | 4 | 1 | 103.11 | 8 | 23206 |
| 4 | 6 | 4 | 2 | 22.01 | 0 | 0 |
| 4 | 6 | 4 | 3 | 18.18 | 1 | 1955 |
| 4 | 6 | 4 | 4 | 3.26 | 0 | 0 |
| 4 | 6 | 4 | 5 | 15.31 | 2 | 5460 |
| 4 | 6 | 4 | 6 | 56.73 | 0 | 0 |
| 4 | 6 | 4 | 7 | 19.28 | 2 | 8463 |
| 4 | 6 | 4 | 8 | 25.32 | 1 | 2735 |
| 4 | 6 | 4 | 9 | 525.48 | 29 | 191633 |
| 4 | 6 | 5 | 1 | 129.17 | 5 | 14134 |
| 4 | 6 | 5 | 2 | 32.33 | 4 | 15546 |
| 4 | 6 | 5 | 3 | 31.20 | 1 | 2965 |
| 4 | 6 | 5 | 4 | 4.05 | 0 | 0 |
| 4 | 6 | 5 | 5 | 29.28 | 0 | 0 |
| 4 | 6 | 5 | 6 | 70.88 | 3 | 36493 |
| 4 | 6 | 5 | 7 | 26.85 | 5 | 10031 |
| 4 | 6 | 5 | 8 | 37.44 | 1 | 6323 |
| 4 | 6 | 5 | 9 | 777.52 | 35 | 203397 |
| 4 | 6 | 6 | 1 | 269.86 | 15 | 75377 |
| 4 | 6 | 6 | 2 | 82.85 | 3 | 5504 |
| 4 | 6 | 6 | 3 | 79.68 | 3 | 9347 |
| 4 | 6 | 6 | 4 | 6.70 | 0 | 0 |
| 4 | 6 | 6 | 5 | 64.77 | 3 | 13395 |
| 4 | 6 | 6 | 6 | 114.70 | 4 | 14816 |
| 4 | 6 | 6 | 7 | 52.70 | 5 | 7421 |
| 4 | 6 | 6 | 8 | 84.33 | 2 | 10085 |
| 4 | 6 | 6 | 9 | 1566.18 | 70 | 289782 |
| 4 | 6 | 7 | 1 | 1647.08 | 55 | 309988 |
| 4 | 6 | 7 | 2 | 477.62 | 23 | 155510 |
| 4 | 6 | 7 | 3 | 484.42 | 20 | 94528 |
| 4 | 6 | 7 | 4 | 35.59 | 1 | 31442 |
| 4 | 6 | 7 | 5 | 335.13 | 16 | 89775 |
| 4 | 6 | 7 | 6 | 731.98 | 10 | 57899 |
| 4 | 6 | 7 | 7 | 314.96 | 7 | 19365 |
| 4 | 6 | 7 | 8 | 568.29 | 24 | 210966 |
| 4 | 6 | 7 | 9 | 9304.84 | 356 | 2121962 |
| 4 | 7 | 1 | 1 | 2.25 | 0 | 0 |
| 4 | 7 | 1 | 2 | 0.09 | 0 | 0 |
| 4 | 7 | 1 | 3 | 0.90 | 0 | 0 |
| 4 | 7 | 1 | 5 | 0.73 | 0 | 0 |
| 4 | 7 | 1 | 6 | 3.46 | 0 | 0 |
| 4 | 7 | 1 | 7 | 0.60 | 0 | 0 |
| 4 | 7 | 1 | 9 | 25.33 | 2 | 4465 |
| 4 | 7 | 2 | 1 | 3.70 | 0 | 0 |
| 4 | 7 | 2 | 2 | 1.21 | 0 | 0 |
| 4 | 7 | 2 | 3 | 0.10 | 0 | 0 |
| 4 | 7 | 2 | 4 | 1.76 | 0 | 0 |
| 4 | 7 | 2 | 5 | 0.50 | 0 | 0 |
| 4 | 7 | 2 | 6 | 4.13 | 1 | 429 |
| 4 | 7 | 2 | 7 | 0.20 | 0 | 0 |
| 4 | 7 | 2 | 9 | 27.70 | 2 | 5216 |
| 4 | 7 | 3 | 1 | 3.23 | 0 | 0 |
| 4 | 7 | 3 | 2 | 1.61 | 0 | 0 |
| 4 | 7 | 3 | 3 | 0.40 | 0 | 0 |
| 4 | 7 | 3 | 5 | 0.70 | 0 | 0 |
| 4 | 7 | 3 | 6 | 5.43 | 1 | 1073 |
| 4 | 7 | 3 | 9 | 31.66 | 3 | 7305 |
| 4 | 7 | 4 | 1 | 4.29 | 1 | 626 |
| 4 | 7 | 4 | 2 | 3.47 | 0 | 0 |
| 4 | 7 | 4 | 3 | 1.49 | 0 | 0 |
| 4 | 7 | 4 | 4 | 0.01 | 0 | 0 |
| 4 | 7 | 4 | 5 | 3.31 | 0 | 0 |
| 4 | 7 | 4 | 6 | 3.27 | 0 | 0 |
| 4 | 7 | 4 | 7 | 0.10 | 0 | 0 |
| 4 | 7 | 4 | 8 | 1.85 | 0 | 0 |
| 4 | 7 | 4 | 9 | 36.11 | 3 | 4855 |
| 4 | 7 | 5 | 1 | 9.89 | 1 | 4125 |
| 4 | 7 | 5 | 2 | 1.50 | 0 | 0 |
| 4 | 7 | 5 | 3 | 0.20 | 0 | 0 |
| 4 | 7 | 5 | 4 | 1.36 | 0 | 0 |
| 4 | 7 | 5 | 5 | 1.77 | 0 | 0 |
| 4 | 7 | 5 | 6 | 2.74 | 0 | 0 |
| 4 | 7 | 5 | 8 | 1.28 | 0 | 0 |
| 4 | 7 | 5 | 9 | 46.95 | 2 | 2864 |
| 4 | 7 | 6 | 1 | 18.06 | 0 | 0 |
| 4 | 7 | 6 | 2 | 5.95 | 0 | 0 |
| 4 | 7 | 6 | 3 | 4.06 | 1 | 1140 |
| 4 | 7 | 6 | 4 | 2.81 | 0 | 0 |
| 4 | 7 | 6 | 5 | 2.70 | 1 | 5000 |
| 4 | 7 | 6 | 6 | 8.08 | 0 | 0 |
| 4 | 7 | 6 | 7 | 2.85 | 0 | 0 |
| 4 | 7 | 6 | 8 | 1.58 | 0 | 0 |
| 4 | 7 | 6 | 9 | 100.73 | 4 | 14546 |
| 4 | 7 | 7 | 1 | 86.76 | 1 | 913 |
| 4 | 7 | 7 | 2 | 36.79 | 3 | 6744 |
| 4 | 7 | 7 | 3 | 12.86 | 0 | 0 |
| 4 | 7 | 7 | 4 | 6.69 | 0 | 0 |
| 4 | 7 | 7 | 5 | 21.03 | 0 | 0 |
| 4 | 7 | 7 | 6 | 38.27 | 0 | 0 |
| 4 | 7 | 7 | 7 | 12.31 | 0 | 0 |
| 4 | 7 | 7 | 8 | 13.59 | 0 | 0 |
| 4 | 7 | 7 | 9 | 661.33 | 15 | 79549 |
| 5 | 1 | 1 | 1 | 39.38 | 8 | 19055 |
| 5 | 1 | 1 | 2 | 33.22 | 14 | 70516 |
| 5 | 1 | 1 | 3 | 25.94 | 6 | 12853 |
| 5 | 1 | 1 | 4 | 4.97 | 0 | 0 |
| 5 | 1 | 1 | 5 | 5.83 | 1 | 5315 |
| 5 | 1 | 1 | 6 | 10.55 | 2 | 14735 |
| 5 | 1 | 1 | 7 | 4.18 | 2 | 3699 |
| 5 | 1 | 1 | 8 | 8.91 | 4 | 2745 |
| 5 | 1 | 1 | 9 | 643.63 | 172 | 802056 |
| 5 | 1 | 2 | 1 | 40.03 | 7 | 53251 |
| 5 | 1 | 2 | 2 | 31.20 | 8 | 64325 |
| 5 | 1 | 2 | 3 | 40.44 | 6 | 51965 |
| 5 | 1 | 2 | 4 | 4.58 | 1 | 8390 |
| 5 | 1 | 2 | 5 | 10.55 | 0 | 0 |
| 5 | 1 | 2 | 6 | 20.21 | 2 | 8498 |
| 5 | 1 | 2 | 7 | 8.99 | 0 | 0 |
| 5 | 1 | 2 | 8 | 7.78 | 2 | 31442 |
| 5 | 1 | 2 | 9 | 697.77 | 122 | 505940 |
| 5 | 1 | 3 | 1 | 54.57 | 8 | 17149 |
| 5 | 1 | 3 | 2 | 36.47 | 8 | 46332 |
| 5 | 1 | 3 | 3 | 32.03 | 6 | 42364 |
| 5 | 1 | 3 | 4 | 4.03 | 0 | 0 |
| 5 | 1 | 3 | 5 | 11.06 | 0 | 0 |
| 5 | 1 | 3 | 6 | 18.96 | 1 | 1000 |
| 5 | 1 | 3 | 7 | 8.71 | 2 | 8327 |
| 5 | 1 | 3 | 8 | 14.50 | 5 | 39056 |
| 5 | 1 | 3 | 9 | 618.16 | 98 | 524453 |
| 5 | 1 | 4 | 1 | 61.37 | 3 | 67055 |
| 5 | 1 | 4 | 2 | 40.59 | 5 | 18027 |
| 5 | 1 | 4 | 3 | 32.00 | 0 | 0 |
| 5 | 1 | 4 | 4 | 2.43 | 0 | 0 |
| 5 | 1 | 4 | 5 | 16.54 | 1 | 1725 |
| 5 | 1 | 4 | 6 | 20.67 | 3 | 10781 |
| 5 | 1 | 4 | 7 | 9.94 | 1 | 3530 |
| 5 | 1 | 4 | 8 | 21.16 | 3 | 3762 |
| 5 | 1 | 4 | 9 | 617.39 | 81 | 449815 |
| 5 | 1 | 5 | 1 | 92.05 | 11 | 18385 |
| 5 | 1 | 5 | 2 | 65.64 | 10 | 47270 |
| 5 | 1 | 5 | 3 | 58.99 | 5 | 40553 |
| 5 | 1 | 5 | 4 | 1.57 | 0 | 0 |
| 5 | 1 | 5 | 5 | 18.46 | 2 | 8860 |
| 5 | 1 | 5 | 6 | 22.92 | 1 | 1845 |
| 5 | 1 | 5 | 7 | 11.36 | 3 | 36029 |
| 5 | 1 | 5 | 8 | 22.87 | 1 | 3801 |
| 5 | 1 | 5 | 9 | 820.04 | 111 | 426845 |
| 5 | 1 | 6 | 1 | 183.54 | 8 | 30510 |
| 5 | 1 | 6 | 2 | 116.62 | 15 | 66600 |
| 5 | 1 | 6 | 3 | 115.02 | 11 | 56739 |
| 5 | 1 | 6 | 4 | 4.61 | 0 | 0 |
| 5 | 1 | 6 | 5 | 42.25 | 4 | 6990 |
| 5 | 1 | 6 | 6 | 47.19 | 4 | 4778 |
| 5 | 1 | 6 | 7 | 23.47 | 1 | 2943 |
| 5 | 1 | 6 | 8 | 55.74 | 8 | 105275 |
| 5 | 1 | 6 | 9 | 1623.22 | 154 | 653118 |
| 5 | 1 | 7 | 1 | 717.63 | 47 | 208573 |
| 5 | 1 | 7 | 2 | 401.42 | 35 | 150942 |
| 5 | 1 | 7 | 3 | 439.61 | 30 | 266009 |
| 5 | 1 | 7 | 4 | 21.22 | 1 | 2000 |
| 5 | 1 | 7 | 5 | 145.24 | 9 | 53228 |
| 5 | 1 | 7 | 6 | 182.52 | 9 | 15099 |
| 5 | 1 | 7 | 7 | 102.40 | 5 | 8972 |
| 5 | 1 | 7 | 8 | 186.24 | 14 | 31626 |
| 5 | 1 | 7 | 9 | 5539.09 | 416 | 2249007 |
| 5 | 2 | 1 | 1 | 43.32 | 4 | 13238 |
| 5 | 2 | 1 | 2 | 21.67 | 5 | 8608 |
| 5 | 2 | 1 | 3 | 21.83 | 1 | 2495 |
| 5 | 2 | 1 | 4 | 6.92 | 2 | 5307 |
| 5 | 2 | 1 | 5 | 9.75 | 1 | 6866 |
| 5 | 2 | 1 | 6 | 20.25 | 0 | 0 |
| 5 | 2 | 1 | 7 | 5.50 | 0 | 0 |
| 5 | 2 | 1 | 8 | 3.68 | 0 | 0 |
| 5 | 2 | 1 | 9 | 451.09 | 87 | 438695 |
| 5 | 2 | 2 | 1 | 53.04 | 10 | 68513 |
| 5 | 2 | 2 | 2 | 26.38 | 4 | 8435 |
| 5 | 2 | 2 | 3 | 29.54 | 3 | 8813 |
| 5 | 2 | 2 | 4 | 6.84 | 0 | 0 |
| 5 | 2 | 2 | 5 | 11.94 | 2 | 3694 |
| 5 | 2 | 2 | 6 | 27.82 | 2 | 4249 |
| 5 | 2 | 2 | 7 | 11.17 | 1 | 2686 |
| 5 | 2 | 2 | 8 | 7.60 | 0 | 0 |
| 5 | 2 | 2 | 9 | 576.16 | 76 | 302181 |
| 5 | 2 | 3 | 1 | 71.90 | 8 | 51707 |
| 5 | 2 | 3 | 2 | 31.96 | 6 | 25061 |
| 5 | 2 | 3 | 3 | 28.18 | 3 | 34674 |
| 5 | 2 | 3 | 4 | 5.98 | 0 | 0 |
| 5 | 2 | 3 | 5 | 10.02 | 2 | 2855 |
| 5 | 2 | 3 | 6 | 22.94 | 1 | 8000 |
| 5 | 2 | 3 | 7 | 13.41 | 1 | 435 |
| 5 | 2 | 3 | 8 | 16.40 | 1 | 4005 |
| 5 | 2 | 3 | 9 | 612.27 | 64 | 228163 |
| 5 | 2 | 4 | 1 | 75.09 | 3 | 12022 |
| 5 | 2 | 4 | 2 | 39.02 | 2 | 3970 |
| 5 | 2 | 4 | 3 | 26.66 | 1 | 1467 |
| 5 | 2 | 4 | 4 | 4.81 | 0 | 0 |
| 5 | 2 | 4 | 5 | 14.32 | 0 | 0 |
| 5 | 2 | 4 | 6 | 38.40 | 1 | 31442 |
| 5 | 2 | 4 | 7 | 15.27 | 2 | 12253 |
| 5 | 2 | 4 | 8 | 19.66 | 2 | 7718 |
| 5 | 2 | 4 | 9 | 703.72 | 91 | 439898 |
| 5 | 2 | 5 | 1 | 122.00 | 2 | 13341 |
| 5 | 2 | 5 | 2 | 49.82 | 4 | 38056 |
| 5 | 2 | 5 | 3 | 56.86 | 0 | 0 |
| 5 | 2 | 5 | 4 | 4.69 | 0 | 0 |
| 5 | 2 | 5 | 5 | 25.10 | 1 | 31442 |
| 5 | 2 | 5 | 6 | 38.73 | 3 | 3731 |
| 5 | 2 | 5 | 7 | 18.83 | 2 | 11144 |
| 5 | 2 | 5 | 8 | 39.01 | 3 | 5673 |
| 5 | 2 | 5 | 9 | 1004.07 | 87 | 547051 |
| 5 | 2 | 6 | 1 | 276.21 | 24 | 84068 |
| 5 | 2 | 6 | 2 | 121.45 | 12 | 40273 |
| 5 | 2 | 6 | 3 | 140.30 | 11 | 72080 |
| 5 | 2 | 6 | 4 | 5.76 | 0 | 0 |
| 5 | 2 | 6 | 5 | 64.51 | 7 | 110527 |
| 5 | 2 | 6 | 6 | 71.49 | 3 | 4822 |
| 5 | 2 | 6 | 7 | 45.13 | 1 | 3571 |
| 5 | 2 | 6 | 8 | 80.96 | 5 | 38993 |
| 5 | 2 | 6 | 9 | 2109.22 | 172 | 625489 |
| 5 | 2 | 7 | 1 | 1110.45 | 65 | 373173 |
| 5 | 2 | 7 | 2 | 484.99 | 43 | 139960 |
| 5 | 2 | 7 | 3 | 611.99 | 34 | 157871 |
| 5 | 2 | 7 | 4 | 31.88 | 0 | 0 |
| 5 | 2 | 7 | 5 | 254.68 | 20 | 147025 |
| 5 | 2 | 7 | 6 | 313.88 | 16 | 102075 |
| 5 | 2 | 7 | 7 | 203.03 | 5 | 14472 |
| 5 | 2 | 7 | 8 | 389.67 | 20 | 141846 |
| 5 | 2 | 7 | 9 | 8729.83 | 517 | 2613039 |
| 5 | 3 | 1 | 1 | 62.53 | 6 | 48495 |
| 5 | 3 | 1 | 2 | 22.94 | 5 | 22703 |
| 5 | 3 | 1 | 3 | 17.73 | 3 | 15788 |
| 5 | 3 | 1 | 4 | 6.76 | 1 | 992 |
| 5 | 3 | 1 | 5 | 8.97 | 2 | 31615 |
| 5 | 3 | 1 | 6 | 25.31 | 3 | 2575 |
| 5 | 3 | 1 | 7 | 7.18 | 3 | 4422 |
| 5 | 3 | 1 | 8 | 4.46 | 2 | 7451 |
| 5 | 3 | 1 | 9 | 440.93 | 54 | 251193 |
| 5 | 3 | 2 | 1 | 74.65 | 12 | 61398 |
| 5 | 3 | 2 | 2 | 21.61 | 1 | 1450 |
| 5 | 3 | 2 | 3 | 27.40 | 3 | 5061 |
| 5 | 3 | 2 | 4 | 5.81 | 2 | 3671 |
| 5 | 3 | 2 | 5 | 13.19 | 2 | 4928 |
| 5 | 3 | 2 | 6 | 32.80 | 5 | 69277 |
| 5 | 3 | 2 | 7 | 11.21 | 0 | 0 |
| 5 | 3 | 2 | 8 | 10.80 | 2 | 2629 |
| 5 | 3 | 2 | 9 | 598.14 | 68 | 264917 |
| 5 | 3 | 3 | 1 | 94.29 | 13 | 54694 |
| 5 | 3 | 3 | 2 | 31.55 | 3 | 34055 |
| 5 | 3 | 3 | 3 | 29.43 | 2 | 1426 |
| 5 | 3 | 3 | 4 | 5.58 | 0 | 0 |
| 5 | 3 | 3 | 5 | 19.91 | 3 | 6534 |
| 5 | 3 | 3 | 6 | 44.03 | 0 | 0 |
| 5 | 3 | 3 | 7 | 16.00 | 2 | 11808 |
| 5 | 3 | 3 | 8 | 11.92 | 0 | 0 |
| 5 | 3 | 3 | 9 | 649.11 | 62 | 329058 |
| 5 | 3 | 4 | 1 | 107.13 | 11 | 94918 |
| 5 | 3 | 4 | 2 | 32.28 | 3 | 2313 |
| 5 | 3 | 4 | 3 | 33.65 | 4 | 12288 |
| 5 | 3 | 4 | 4 | 3.27 | 0 | 0 |
| 5 | 3 | 4 | 5 | 22.77 | 3 | 5911 |
| 5 | 3 | 4 | 6 | 43.27 | 2 | 10115 |
| 5 | 3 | 4 | 7 | 12.37 | 1 | 3392 |
| 5 | 3 | 4 | 8 | 21.73 | 0 | 0 |
| 5 | 3 | 4 | 9 | 729.80 | 63 | 235765 |
| 5 | 3 | 5 | 1 | 149.79 | 8 | 37006 |
| 5 | 3 | 5 | 2 | 58.08 | 5 | 37990 |
| 5 | 3 | 5 | 3 | 48.59 | 6 | 11364 |
| 5 | 3 | 5 | 4 | 6.96 | 0 | 0 |
| 5 | 3 | 5 | 5 | 34.25 | 4 | 35822 |
| 5 | 3 | 5 | 6 | 59.82 | 4 | 6347 |
| 5 | 3 | 5 | 7 | 23.38 | 2 | 6534 |
| 5 | 3 | 5 | 8 | 44.65 | 3 | 4969 |
| 5 | 3 | 5 | 9 | 1054.73 | 69 | 281281 |
| 5 | 3 | 6 | 1 | 300.28 | 22 | 76756 |
| 5 | 3 | 6 | 2 | 124.65 | 12 | 92958 |
| 5 | 3 | 6 | 3 | 145.50 | 5 | 19178 |
| 5 | 3 | 6 | 4 | 9.91 | 0 | 0 |
| 5 | 3 | 6 | 5 | 63.07 | 5 | 20281 |
| 5 | 3 | 6 | 6 | 101.73 | 6 | 43173 |
| 5 | 3 | 6 | 7 | 51.13 | 7 | 28491 |
| 5 | 3 | 6 | 8 | 116.28 | 4 | 7403 |
| 5 | 3 | 6 | 9 | 2084.66 | 159 | 771665 |
| 5 | 3 | 7 | 1 | 1291.25 | 41 | 293493 |
| 5 | 3 | 7 | 2 | 520.94 | 29 | 138830 |
| 5 | 3 | 7 | 3 | 676.38 | 28 | 235831 |
| 5 | 3 | 7 | 4 | 35.33 | 2 | 5829 |
| 5 | 3 | 7 | 5 | 299.99 | 23 | 120261 |
| 5 | 3 | 7 | 6 | 523.39 | 14 | 62013 |
| 5 | 3 | 7 | 7 | 265.89 | 13 | 36704 |
| 5 | 3 | 7 | 8 | 599.43 | 29 | 155051 |
| 5 | 3 | 7 | 9 | 9965.28 | 486 | 2560945 |
| 5 | 4 | 1 | 1 | 109.23 | 13 | 60096 |
| 5 | 4 | 1 | 2 | 31.71 | 3 | 36934 |
| 5 | 4 | 1 | 3 | 32.35 | 2 | 32365 |
| 5 | 4 | 1 | 4 | 9.88 | 1 | 3542 |
| 5 | 4 | 1 | 5 | 19.48 | 2 | 1065 |
| 5 | 4 | 1 | 6 | 50.65 | 5 | 42686 |
| 5 | 4 | 1 | 7 | 16.11 | 4 | 7357 |
| 5 | 4 | 1 | 8 | 15.57 | 1 | 9579 |
| 5 | 4 | 1 | 9 | 770.69 | 91 | 524705 |
| 5 | 4 | 2 | 1 | 180.10 | 26 | 103992 |
| 5 | 4 | 2 | 2 | 35.50 | 5 | 65836 |
| 5 | 4 | 2 | 3 | 50.22 | 2 | 32896 |
| 5 | 4 | 2 | 4 | 11.90 | 1 | 2825 |
| 5 | 4 | 2 | 5 | 36.25 | 6 | 11558 |
| 5 | 4 | 2 | 6 | 106.18 | 7 | 21782 |
| 5 | 4 | 2 | 7 | 22.34 | 1 | 7660 |
| 5 | 4 | 2 | 8 | 25.02 | 3 | 6659 |
| 5 | 4 | 2 | 9 | 1141.56 | 115 | 557417 |
| 5 | 4 | 3 | 1 | 198.57 | 18 | 70984 |
| 5 | 4 | 3 | 2 | 59.81 | 3 | 14822 |
| 5 | 4 | 3 | 3 | 46.93 | 2 | 4836 |
| 5 | 4 | 3 | 4 | 14.15 | 0 | 0 |
| 5 | 4 | 3 | 5 | 35.34 | 1 | 1985 |
| 5 | 4 | 3 | 6 | 106.79 | 5 | 40142 |
| 5 | 4 | 3 | 7 | 25.13 | 3 | 9201 |
| 5 | 4 | 3 | 8 | 34.61 | 1 | 1753 |
| 5 | 4 | 3 | 9 | 1219.62 | 113 | 506246 |
| 5 | 4 | 4 | 1 | 230.03 | 9 | 53377 |
| 5 | 4 | 4 | 2 | 59.93 | 4 | 15865 |
| 5 | 4 | 4 | 3 | 47.93 | 1 | 31442 |
| 5 | 4 | 4 | 4 | 12.54 | 1 | 800 |
| 5 | 4 | 4 | 5 | 34.38 | 1 | 2237 |
| 5 | 4 | 4 | 6 | 107.54 | 7 | 50019 |
| 5 | 4 | 4 | 7 | 31.52 | 5 | 19379 |
| 5 | 4 | 4 | 8 | 56.83 | 2 | 3886 |
| 5 | 4 | 4 | 9 | 1419.58 | 99 | 647293 |
| 5 | 4 | 5 | 1 | 317.01 | 15 | 80540 |
| 5 | 4 | 5 | 2 | 104.40 | 5 | 10570 |
| 5 | 4 | 5 | 3 | 102.93 | 4 | 5590 |
| 5 | 4 | 5 | 4 | 10.46 | 0 | 0 |
| 5 | 4 | 5 | 5 | 50.41 | 2 | 4525 |
| 5 | 4 | 5 | 6 | 122.58 | 5 | 16623 |
| 5 | 4 | 5 | 7 | 47.24 | 5 | 11325 |
| 5 | 4 | 5 | 8 | 92.60 | 8 | 43023 |
| 5 | 4 | 5 | 9 | 2014.55 | 125 | 644099 |
| 5 | 4 | 6 | 1 | 541.77 | 32 | 161900 |
| 5 | 4 | 6 | 2 | 215.82 | 6 | 14288 |
| 5 | 4 | 6 | 3 | 246.80 | 8 | 58500 |
| 5 | 4 | 6 | 4 | 11.39 | 0 | 0 |
| 5 | 4 | 6 | 5 | 133.59 | 13 | 95129 |
| 5 | 4 | 6 | 6 | 226.28 | 10 | 22795 |
| 5 | 4 | 6 | 7 | 107.83 | 8 | 25329 |
| 5 | 4 | 6 | 8 | 242.78 | 15 | 168380 |
| 5 | 4 | 6 | 9 | 4231.59 | 250 | 1304846 |
| 5 | 4 | 7 | 1 | 2946.70 | 122 | 613652 |
| 5 | 4 | 7 | 2 | 1117.96 | 58 | 255116 |
| 5 | 4 | 7 | 3 | 1396.49 | 53 | 337846 |
| 5 | 4 | 7 | 4 | 75.39 | 1 | 1962 |
| 5 | 4 | 7 | 5 | 635.91 | 29 | 196401 |
| 5 | 4 | 7 | 6 | 1291.12 | 50 | 333231 |
| 5 | 4 | 7 | 7 | 542.86 | 23 | 91399 |
| 5 | 4 | 7 | 8 | 1382.66 | 52 | 571579 |
| 5 | 4 | 7 | 9 | 21581.24 | 920 | 4847989 |
| 5 | 5 | 1 | 1 | 9.75 | 0 | 0 |
| 5 | 5 | 1 | 2 | 2.94 | 0 | 0 |
| 5 | 5 | 1 | 3 | 14.21 | 3 | 13529 |
| 5 | 5 | 1 | 4 | 0.76 | 0 | 0 |
| 5 | 5 | 1 | 5 | 3.42 | 1 | 4058 |
| 5 | 5 | 1 | 6 | 5.64 | 0 | 0 |
| 5 | 5 | 1 | 7 | 2.44 | 0 | 0 |
| 5 | 5 | 1 | 8 | 2.49 | 1 | 31442 |
| 5 | 5 | 1 | 9 | 117.39 | 17 | 121307 |
| 5 | 5 | 2 | 1 | 17.77 | 0 | 0 |
| 5 | 5 | 2 | 2 | 4.89 | 1 | 9007 |
| 5 | 5 | 2 | 3 | 4.58 | 0 | 0 |
| 5 | 5 | 2 | 4 | 0.10 | 0 | 0 |
| 5 | 5 | 2 | 5 | 6.13 | 1 | 4225 |
| 5 | 5 | 2 | 6 | 5.16 | 0 | 0 |
| 5 | 5 | 2 | 7 | 2.39 | 0 | 0 |
| 5 | 5 | 2 | 8 | 3.41 | 0 | 0 |
| 5 | 5 | 2 | 9 | 140.20 | 13 | 95879 |
| 5 | 5 | 3 | 1 | 20.03 | 0 | 0 |
| 5 | 5 | 3 | 2 | 6.06 | 0 | 0 |
| 5 | 5 | 3 | 3 | 3.24 | 1 | 779 |
| 5 | 5 | 3 | 4 | 1.16 | 0 | 0 |
| 5 | 5 | 3 | 5 | 1.52 | 0 | 0 |
| 5 | 5 | 3 | 6 | 9.01 | 0 | 0 |
| 5 | 5 | 3 | 7 | 2.63 | 0 | 0 |
| 5 | 5 | 3 | 8 | 10.94 | 2 | 6484 |
| 5 | 5 | 3 | 9 | 188.15 | 13 | 75374 |
| 5 | 5 | 4 | 1 | 20.61 | 3 | 35174 |
| 5 | 5 | 4 | 2 | 7.09 | 0 | 0 |
| 5 | 5 | 4 | 3 | 7.60 | 2 | 3611 |
| 5 | 5 | 4 | 5 | 3.31 | 0 | 0 |
| 5 | 5 | 4 | 6 | 13.00 | 0 | 0 |
| 5 | 5 | 4 | 7 | 1.37 | 0 | 0 |
| 5 | 5 | 4 | 8 | 11.07 | 0 | 0 |
| 5 | 5 | 4 | 9 | 177.36 | 12 | 61341 |
| 5 | 5 | 5 | 1 | 28.28 | 1 | 716 |
| 5 | 5 | 5 | 2 | 17.99 | 1 | 3896 |
| 5 | 5 | 5 | 3 | 21.19 | 1 | 1576 |
| 5 | 5 | 5 | 5 | 10.13 | 0 | 0 |
| 5 | 5 | 5 | 6 | 10.81 | 0 | 0 |
| 5 | 5 | 5 | 7 | 3.99 | 0 | 0 |
| 5 | 5 | 5 | 8 | 12.05 | 0 | 0 |
| 5 | 5 | 5 | 9 | 234.00 | 22 | 107065 |
| 5 | 5 | 6 | 1 | 54.72 | 1 | 3000 |
| 5 | 5 | 6 | 2 | 21.61 | 2 | 4502 |
| 5 | 5 | 6 | 3 | 42.44 | 2 | 3695 |
| 5 | 5 | 6 | 4 | 1.65 | 0 | 0 |
| 5 | 5 | 6 | 5 | 16.46 | 0 | 0 |
| 5 | 5 | 6 | 6 | 26.23 | 2 | 10259 |
| 5 | 5 | 6 | 7 | 13.65 | 3 | 5598 |
| 5 | 5 | 6 | 8 | 39.76 | 4 | 15915 |
| 5 | 5 | 6 | 9 | 568.65 | 42 | 186899 |
| 5 | 5 | 7 | 1 | 266.04 | 17 | 80318 |
| 5 | 5 | 7 | 2 | 116.75 | 6 | 48119 |
| 5 | 5 | 7 | 3 | 171.84 | 9 | 26797 |
| 5 | 5 | 7 | 4 | 2.07 | 0 | 0 |
| 5 | 5 | 7 | 5 | 61.96 | 4 | 10580 |
| 5 | 5 | 7 | 6 | 114.36 | 2 | 39981 |
| 5 | 5 | 7 | 7 | 49.37 | 2 | 5391 |
| 5 | 5 | 7 | 8 | 173.28 | 11 | 119909 |
| 5 | 5 | 7 | 9 | 2387.46 | 99 | 559278 |
| 5 | 6 | 1 | 1 | 30.80 | 4 | 8714 |
| 5 | 6 | 1 | 2 | 11.97 | 2 | 7747 |
| 5 | 6 | 1 | 3 | 3.22 | 1 | 31442 |
| 5 | 6 | 1 | 4 | 1.34 | 0 | 0 |
| 5 | 6 | 1 | 5 | 8.91 | 2 | 3112 |
| 5 | 6 | 1 | 6 | 15.68 | 0 | 0 |
| 5 | 6 | 1 | 7 | 6.17 | 0 | 0 |
| 5 | 6 | 1 | 8 | 6.94 | 1 | 994 |
| 5 | 6 | 1 | 9 | 201.95 | 15 | 120724 |
| 5 | 6 | 2 | 1 | 62.69 | 9 | 20731 |
| 5 | 6 | 2 | 2 | 8.04 | 0 | 0 |
| 5 | 6 | 2 | 3 | 10.73 | 0 | 0 |
| 5 | 6 | 2 | 4 | 1.68 | 0 | 0 |
| 5 | 6 | 2 | 5 | 15.42 | 1 | 3277 |
| 5 | 6 | 2 | 6 | 31.15 | 2 | 5291 |
| 5 | 6 | 2 | 7 | 9.18 | 1 | 4884 |
| 5 | 6 | 2 | 8 | 10.16 | 0 | 0 |
| 5 | 6 | 2 | 9 | 316.66 | 21 | 119632 |
| 5 | 6 | 3 | 1 | 63.63 | 2 | 5400 |
| 5 | 6 | 3 | 2 | 11.93 | 2 | 9525 |
| 5 | 6 | 3 | 3 | 12.55 | 0 | 0 |
| 5 | 6 | 3 | 4 | 2.30 | 0 | 0 |
| 5 | 6 | 3 | 5 | 10.67 | 1 | 31442 |
| 5 | 6 | 3 | 6 | 38.64 | 2 | 1953 |
| 5 | 6 | 3 | 7 | 13.39 | 3 | 9508 |
| 5 | 6 | 3 | 8 | 12.02 | 1 | 4581 |
| 5 | 6 | 3 | 9 | 359.57 | 26 | 139072 |
| 5 | 6 | 4 | 1 | 69.43 | 11 | 62295 |
| 5 | 6 | 4 | 2 | 13.47 | 1 | 2575 |
| 5 | 6 | 4 | 3 | 14.11 | 2 | 32158 |
| 5 | 6 | 4 | 4 | 1.05 | 0 | 0 |
| 5 | 6 | 4 | 5 | 7.50 | 1 | 31442 |
| 5 | 6 | 4 | 6 | 36.19 | 0 | 0 |
| 5 | 6 | 4 | 7 | 8.58 | 1 | 1135 |
| 5 | 6 | 4 | 8 | 22.65 | 1 | 3590 |
| 5 | 6 | 4 | 9 | 393.00 | 24 | 116662 |
| 5 | 6 | 5 | 1 | 87.44 | 5 | 17072 |
| 5 | 6 | 5 | 2 | 23.03 | 2 | 2283 |
| 5 | 6 | 5 | 3 | 23.02 | 0 | 0 |
| 5 | 6 | 5 | 4 | 1.58 | 0 | 0 |
| 5 | 6 | 5 | 5 | 10.55 | 2 | 32423 |
| 5 | 6 | 5 | 6 | 32.49 | 5 | 68672 |
| 5 | 6 | 5 | 7 | 10.74 | 0 | 0 |
| 5 | 6 | 5 | 8 | 32.78 | 0 | 0 |
| 5 | 6 | 5 | 9 | 533.49 | 36 | 186668 |
| 5 | 6 | 6 | 1 | 157.06 | 5 | 16138 |
| 5 | 6 | 6 | 2 | 49.35 | 3 | 64610 |
| 5 | 6 | 6 | 3 | 67.45 | 2 | 2977 |
| 5 | 6 | 6 | 4 | 1.15 | 0 | 0 |
| 5 | 6 | 6 | 5 | 39.60 | 1 | 1802 |
| 5 | 6 | 6 | 6 | 75.36 | 2 | 11385 |
| 5 | 6 | 6 | 7 | 25.64 | 1 | 1968 |
| 5 | 6 | 6 | 8 | 102.98 | 7 | 46010 |
| 5 | 6 | 6 | 9 | 1203.01 | 65 | 389080 |
| 5 | 6 | 7 | 1 | 889.43 | 34 | 261859 |
| 5 | 6 | 7 | 2 | 313.49 | 18 | 137743 |
| 5 | 6 | 7 | 3 | 415.78 | 11 | 79125 |
| 5 | 6 | 7 | 4 | 19.50 | 1 | 874 |
| 5 | 6 | 7 | 5 | 178.83 | 10 | 21659 |
| 5 | 6 | 7 | 6 | 389.82 | 17 | 64534 |
| 5 | 6 | 7 | 7 | 147.94 | 7 | 24026 |
| 5 | 6 | 7 | 8 | 579.49 | 29 | 130489 |
| 5 | 6 | 7 | 9 | 6392.60 | 317 | 1517683 |
| 5 | 7 | 1 | 1 | 0.90 | 0 | 0 |
| 5 | 7 | 1 | 2 | 0.04 | 0 | 0 |
| 5 | 7 | 1 | 5 | 0.70 | 0 | 0 |
| 5 | 7 | 1 | 9 | 14.77 | 2 | 8628 |
| 5 | 7 | 2 | 1 | 2.25 | 0 | 0 |
| 5 | 7 | 2 | 2 | 0.72 | 0 | 0 |
| 5 | 7 | 2 | 3 | 0.46 | 0 | 0 |
| 5 | 7 | 2 | 5 | 0.30 | 0 | 0 |
| 5 | 7 | 2 | 6 | 1.32 | 0 | 0 |
| 5 | 7 | 2 | 7 | 0.46 | 0 | 0 |
| 5 | 7 | 2 | 9 | 27.54 | 1 | 1314 |
| 5 | 7 | 3 | 1 | 4.71 | 0 | 0 |
| 5 | 7 | 3 | 2 | 1.88 | 0 | 0 |
| 5 | 7 | 3 | 3 | 0.08 | 0 | 0 |
| 5 | 7 | 3 | 5 | 0.04 | 0 | 0 |
| 5 | 7 | 3 | 6 | 1.88 | 0 | 0 |
| 5 | 7 | 3 | 7 | 0.58 | 0 | 0 |
| 5 | 7 | 3 | 9 | 23.65 | 2 | 6600 |
| 5 | 7 | 4 | 1 | 3.74 | 0 | 0 |
| 5 | 7 | 4 | 2 | 1.20 | 0 | 0 |
| 5 | 7 | 4 | 4 | 0.70 | 0 | 0 |
| 5 | 7 | 4 | 6 | 0.96 | 1 | 1231 |
| 5 | 7 | 4 | 7 | 0.03 | 0 | 0 |
| 5 | 7 | 4 | 9 | 24.61 | 0 | 0 |
| 5 | 7 | 5 | 1 | 5.98 | 2 | 6102 |
| 5 | 7 | 5 | 2 | 0.80 | 0 | 0 |
| 5 | 7 | 5 | 3 | 1.10 | 0 | 0 |
| 5 | 7 | 5 | 4 | 0.34 | 0 | 0 |
| 5 | 7 | 5 | 5 | 0.70 | 0 | 0 |
| 5 | 7 | 5 | 6 | 2.48 | 0 | 0 |
| 5 | 7 | 5 | 7 | 0.60 | 1 | 2935 |
| 5 | 7 | 5 | 8 | 1.14 | 0 | 0 |
| 5 | 7 | 5 | 9 | 38.77 | 1 | 1150 |
| 5 | 7 | 6 | 1 | 8.47 | 0 | 0 |
| 5 | 7 | 6 | 2 | 2.49 | 0 | 0 |
| 5 | 7 | 6 | 3 | 2.89 | 0 | 0 |
| 5 | 7 | 6 | 4 | 0.13 | 0 | 0 |
| 5 | 7 | 6 | 5 | 1.36 | 0 | 0 |
| 5 | 7 | 6 | 6 | 4.15 | 0 | 0 |
| 5 | 7 | 6 | 7 | 2.23 | 0 | 0 |
| 5 | 7 | 6 | 8 | 1.96 | 0 | 0 |
| 5 | 7 | 6 | 9 | 69.70 | 2 | 32275 |
| 5 | 7 | 7 | 1 | 51.24 | 1 | 31442 |
| 5 | 7 | 7 | 2 | 21.74 | 2 | 31942 |
| 5 | 7 | 7 | 3 | 9.91 | 0 | 0 |
| 5 | 7 | 7 | 4 | 2.35 | 0 | 0 |
| 5 | 7 | 7 | 5 | 8.74 | 0 | 0 |
| 5 | 7 | 7 | 6 | 16.61 | 0 | 0 |
| 5 | 7 | 7 | 7 | 2.83 | 1 | 966 |
| 5 | 7 | 7 | 8 | 13.06 | 0 | 0 |
| 5 | 7 | 7 | 9 | 384.87 | 16 | 112252 |
Os gráficos abaixo fornecem uma descritiva do conjunto de dados:
g1 <- ggplot(data = insurance, aes(x = Payment)) +
geom_density() +
geom_histogram(aes(y = ..density..))
g2 <- ggplot(data = insurance, aes(x = Insured, y = Payment)) +
geom_point()
gridExtra::grid.arrange(g1, g2, ncol = 2)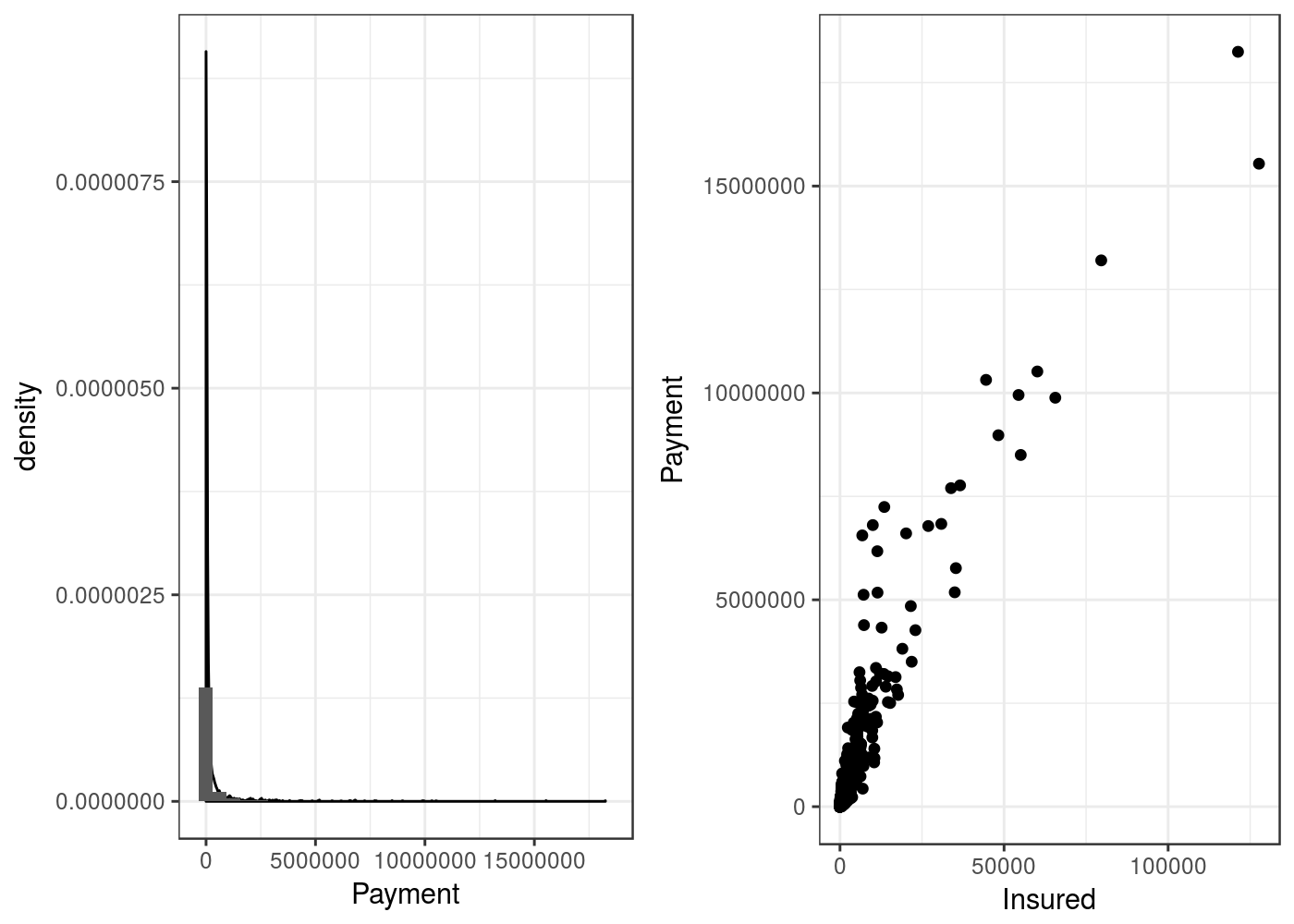
O gráfico da esquerda apresenta a densidade para a variável resposta (total de pagamentos) e o gráfico da direita mostra o diagrama de dispersão entre o total de pagamentos e a fração de anos do segurado.
O gráfico da esquerda apresenta uma densidade acentuada para valores de pagamentos iguais a 0, bem como uma cauda pesada da distribuição. Já o gráfico da direita mostra que a relação de ambas variáveis não é linear, e além disso, não pode assumir valores negativos (uma vez que ambas variáveis pertencem aos reais positivos).
Aqui, iremos utilizar uma curva suave para a covariável Insured cujo suavizador a ser utilizado será uma regressão cúbica spline com janela igual a 100 dados, além do parâmetro de potência da tweedie que será estimado via máxima verossimilhança. Foi necessário mudar a janela \(k\) nesse caso, devida a alta concentação de pontos próximos de 0, e pequena concentração de pontos a medida que se distância de zero. Ainda, a escolha de um suavizador cúbico, por ser mais flexível que o default (plate regression spline) acomodou melhor o padrão dos dados. Segue resultados na escala do preditor linear (saída padrão do mgcv):
m1 <- mgcv::gam(Payment ~ s(Insured, bs = "cr", k = 100), data = insurance, family = mgcv::tw())
# summary(m1)
plot(m1)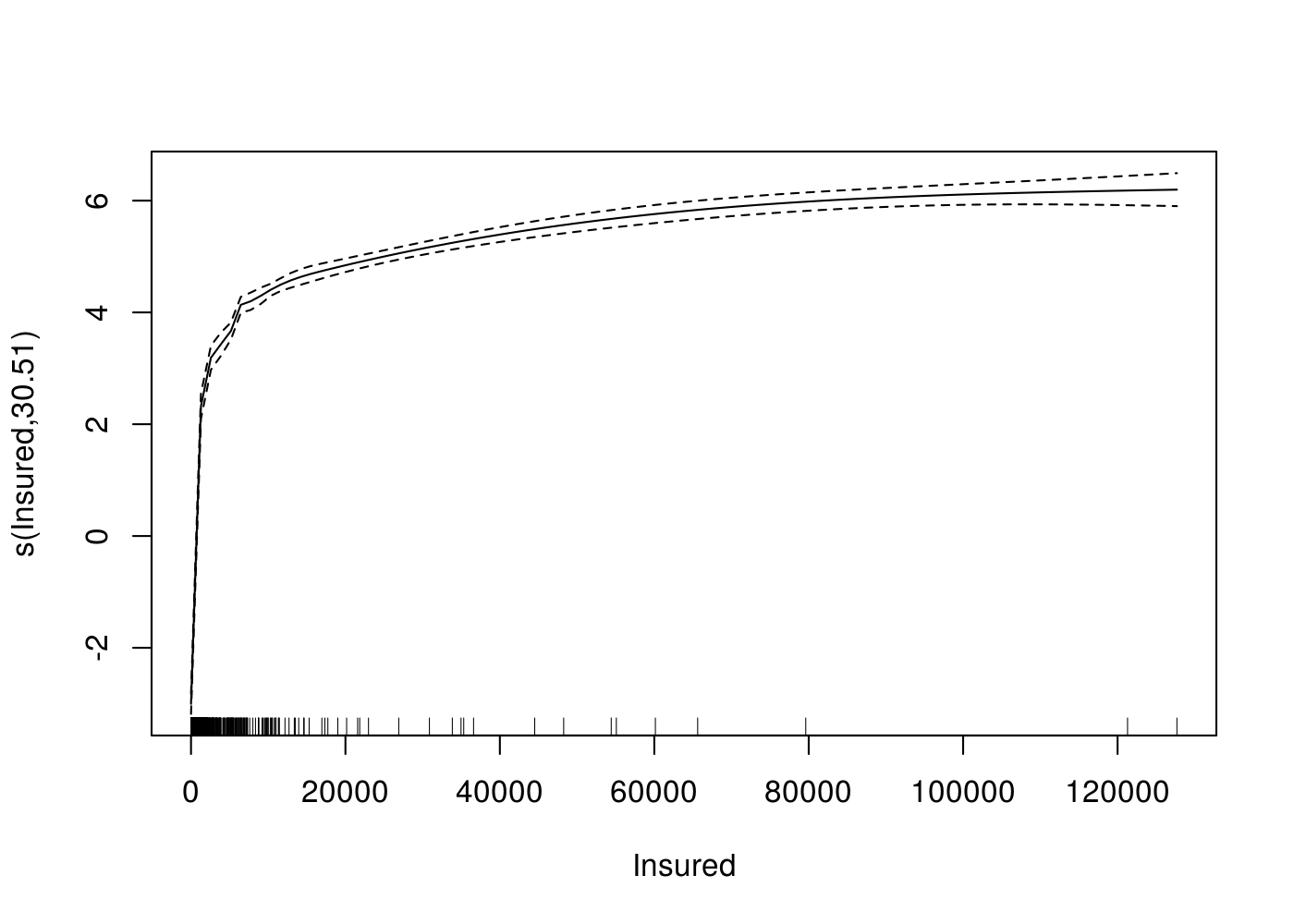
Segue resultado na escala da varíavel resposta com banda de confiança tipo Wald:
nd <- data.frame(Insured = insurance$Insured)
a1 <- mgcv::predict.gam(m1, newdata = nd, type = "response", se.fit = T)
a1 <- plyr::ldply(a1, data.frame)
a1$sub <- factor(rep(1:(nrow(a1)/2), times = 2))
a1 <- reshape2::dcast(a1, sub ~ .id, FUN = sum, value.var = "X..i..")
a1$fit.min <- a1$fit - a1$se
a1$fit.max <- a1$fit + a1$se
a1$x <- insurance$Insured
ggplot(data = a1, aes(x = x, y = fit)) +
geom_line() +
geom_ribbon(aes(ymin = fit.min, ymax = fit.max),
alpha = 0.1) +
geom_point(data = insurance, aes(x = Insured, y = Payment)) +
labs(x = "Insured",
y = "Payment")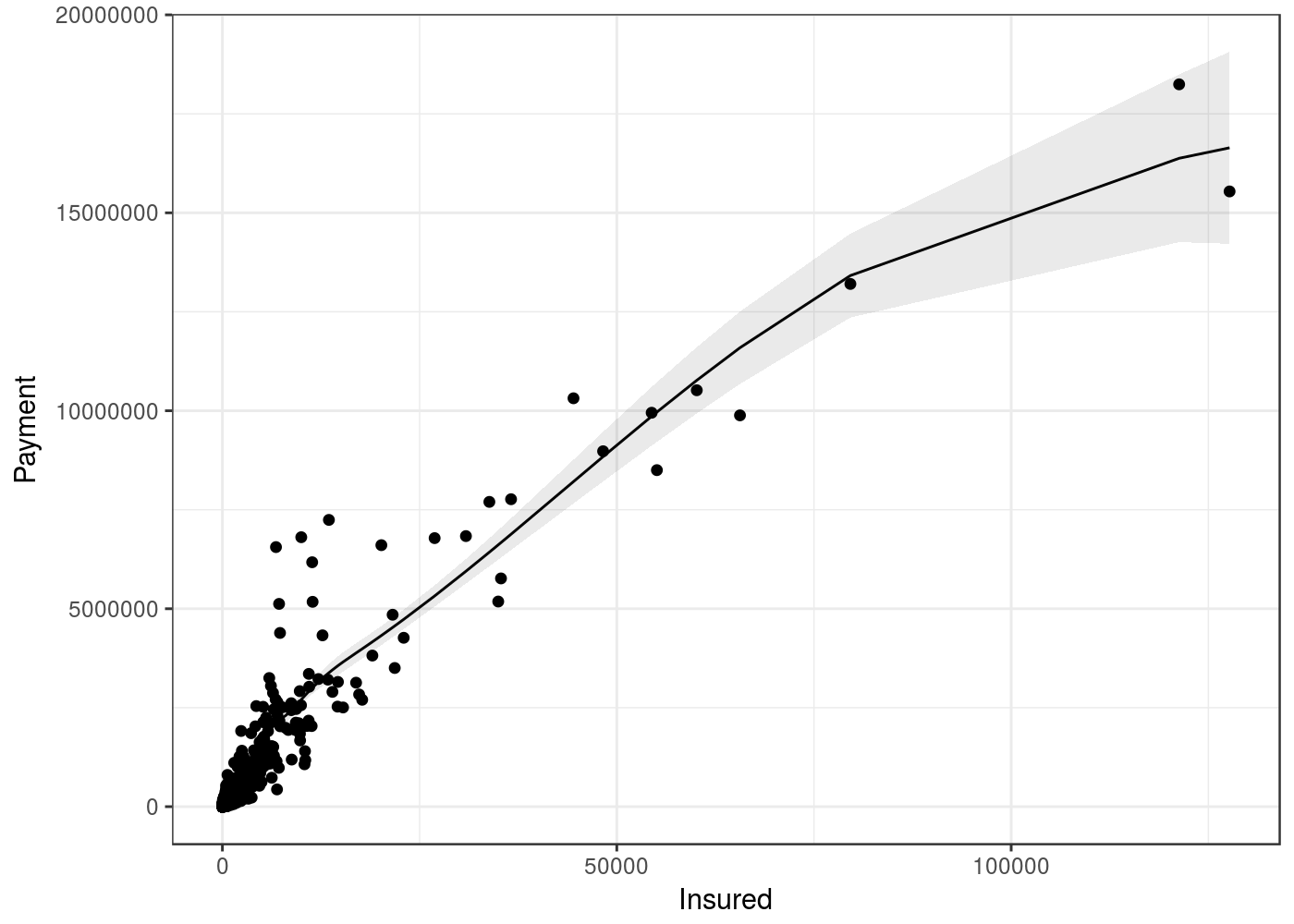
Nota-se que a curva ajustada acompanha o comportamento dos dados, e melhor, a curva não assume valores negativos, por conta da restrição da distribuição Tweedie.
Conclusão
Nós vimos que a distribuição Tweedie é bem flexível, pois é possível acomodar valores assimétricos que contém 0, e as formas dessa distribuição para alguns valores de p coincidem com distribuições mais conhecidas (como a normal e gamma). Ainda, o uso dela em contexto de modelos de regressão é viável tanto na função glm como na mgcv::gam.
É isso aí pessoal! Espero que tenham gostado! Até a próxima.
Referências
BONAT, W. H. mcglm: Multivariate Covariance Generalized Linear Models. Traducao. [s.l: s.n.].
BONAT, W. H.; JØRGENSEN, B. Multivariate covariance generalized linear models. Journal of the Royal Statistical Society: Series C (Applied Statistics), v. 65, n. 5, p. 649–675, 2016.
FREES, E. W. Regression modeling with actuarial and financial applications. Traducao. [s.l.] Cambridge University Press, 2009.

