[Guilherme Parreira] | May 15, 2018
No post de hoje, iremos tratar sobre um dos coeficientes mais comum e amplamente utilizados: o coeficiente de correlação de Pearson.
Basicamente, calcula-se o coeficiente de correlação de Pearson quando duas variáveis são ditas como numéricas (isto é, quando elas são intervalares) e têm-se o interesse de saber o quanto a variabilidade de uma variável está correlacionada com a variabilidade de outra variável.
O coeficiente de correlação de Pearson (r) varia entre -1 e +1, cujos valores próximos de -1 e +1 indicam forte correlação linear e próximos de 0 indicam ausência de correlação linear. Note que ele capta apenas relações lineares entre variáveis (quaisquer outras relações, tal coeficiente não é indicado: isso será exemplificado na sequência).
Note que entre 0 e 1, existe uma grande gama de valores que o coeficiente pode assumir. Para tal, diferentes autores buscaram dar “nomes” aos diferentes valores que o coeficiente de correlação pode assumir, para poder dizer se um dado valor de correlação pode ser dito como fraco/moderada/forte. Sob o meu ponto de vista, que é puramente estatístico (e de não consenso entre os estatísticos), pode-se obter uma relação da seguinte forma:
| Coeficiente de Correlação | Classificação |
|---|---|
| 0 < r \(\leq\) |0,1| | Nula |
| |0,1| < r \(\leq\) |0,3| | Fraca |
| |0,3| < r \(\leq\) |0,6| | Moderada |
| |0,6| < r \(\leq\) |0,9| | Forte |
| |0,9| < r < |1| | Muito Forte |
| r = 1 | Perfeita |
Caso o valor calculado de r = 0,3, pode-se “concluir” que a correlação entre as variáveis foi fraca. No entanto, note que essa tabela foi feita de forma “arbitrária”, sem levar em consideração o contexto do estudo. Na realidade, toda e qualquer tabela que tente categorizar os valores para algum coeficiente de correlação foi criada de forma arbitrária, isto é, sem critério científico, baseada apenas no conhecimento do autor da tabela. Não existe estudo que seja possível afirmar que um valor = 0,4 é fraco/moderado/forte. Vamos supor que temos o objetivo de avaliar qual índice está correlacionado com os pontos da ibovespa. Pelo fato da IBOVESPA ser um índice com alta volatilidade (alta variabilidade), e com um pouco de background da área de negócios, sabe-se que é muito difícil alguma outra variável estar correlacionada com a série da IBOVESPA (caso contrário, a maioria apostaria na bolsa). Dessa forma, um valor de correlação igual a 0,30, por mais que seja pequeno (sob o ponto de vista estatístico), para a área pode ser tido como “forte”, pois ela é a que melhor explica a relação entre a IBOVESPA e a outra variável. Por outro lado, uma correlação entre peso e altura espera-sse que seja “alta”, e na maioria dos casos, é “alta”; assim como IMC e Peso (uma vez que IMC é função do Peso). A próxima tabela apresenta a categorização adaptada de CALLEGARI-JACQUES (2009).
| Coeficiente de Correlação | Classificação |
|---|---|
| r = 0 | Nula |
| 0 < r \(\leq\) |0,3| | Fraca |
| |0,3| < r \(\leq\) |0,6| | Moderada |
| |0,6| < r \(\leq\) |0,9| | Forte |
| |0,9| < r < |1| | Muito Forte |
| r = 1 | Perfeita |
Nota-se que é uma tabela muito próxima da que eu sugeri, e diferentes autores podem sugerir ainda diferentes outras tabelas. Agora vamos colocar a mão na massa para entender melhor os diferentes valores de correlação! Foram criados (simulados) dados para uma variável qualquer X e para uma variável Y estabelecendo diferentes valores de correlação. Os dados criados são apresentados no diagrama de dispersão:
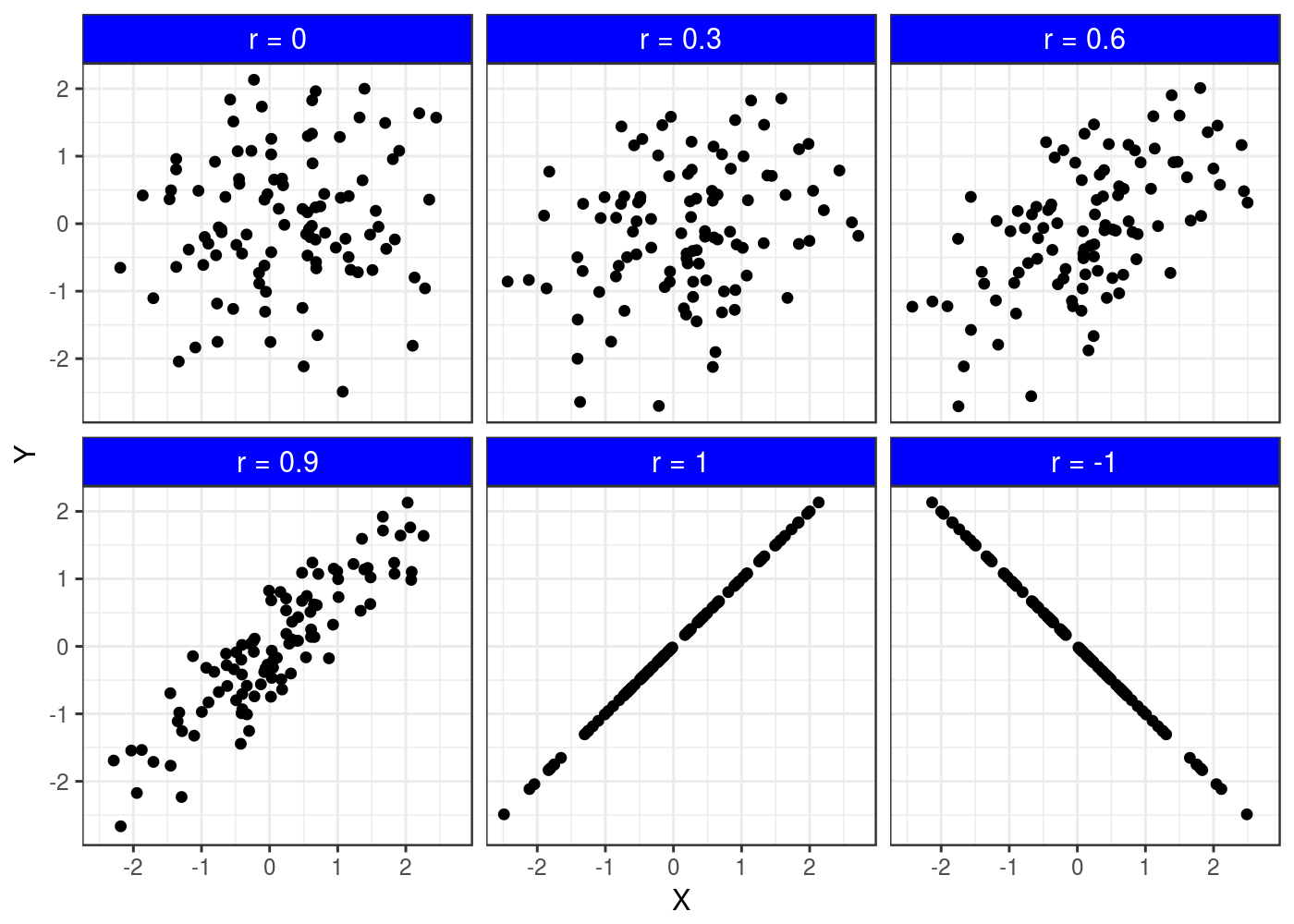
Note que quando r = 0, o gráfico torna-se a forma da qual chamamos de nuvem de pontos, ou seja, os pontos parecem estar bem embaralhados (sem direção). Quando r = 0,3, os dados já começam a ter uma inclinação em um único sentido, mas note que ainda tem muitos pontos fora de uma “reta imaginária”. Quando r = 0.6, os pontos começam a ficar um pouco mais próximos e menos dispersos, o mesmo ocorre para r = 0.9. E finalmente quando r = 1, nota-se que os pontos coincidem exatamente com o formato de uma reta, tornando-se assim, uma correlação perfeita. Exceto quando r = 0, a interpretação pode ser feita da seguinte forma: maiores valores da variável X estão associados com maiores valores da variável Y. Para r = 0, pode-se dizer que não existe correlação. Quando r = -1, nota-se que também tem uma correlação perfeita, só que nesse caso, negativa, ou seja, maiores valores de uma variável, estão correlacionados com menores valores da outra variável, e vice-versa.
O site http://guessthecorrelation.com/ oferece uma interface para que o usuário adivinhe a correlação entre duas variáveis, e assim, podemos melhorar a nossa capacidade de interpretar gráficos desse tipo e acertar nossos “chutes” quanto ao valor da correlação.
Agora, nota-se a relação entre as duas variáveis seguintes:
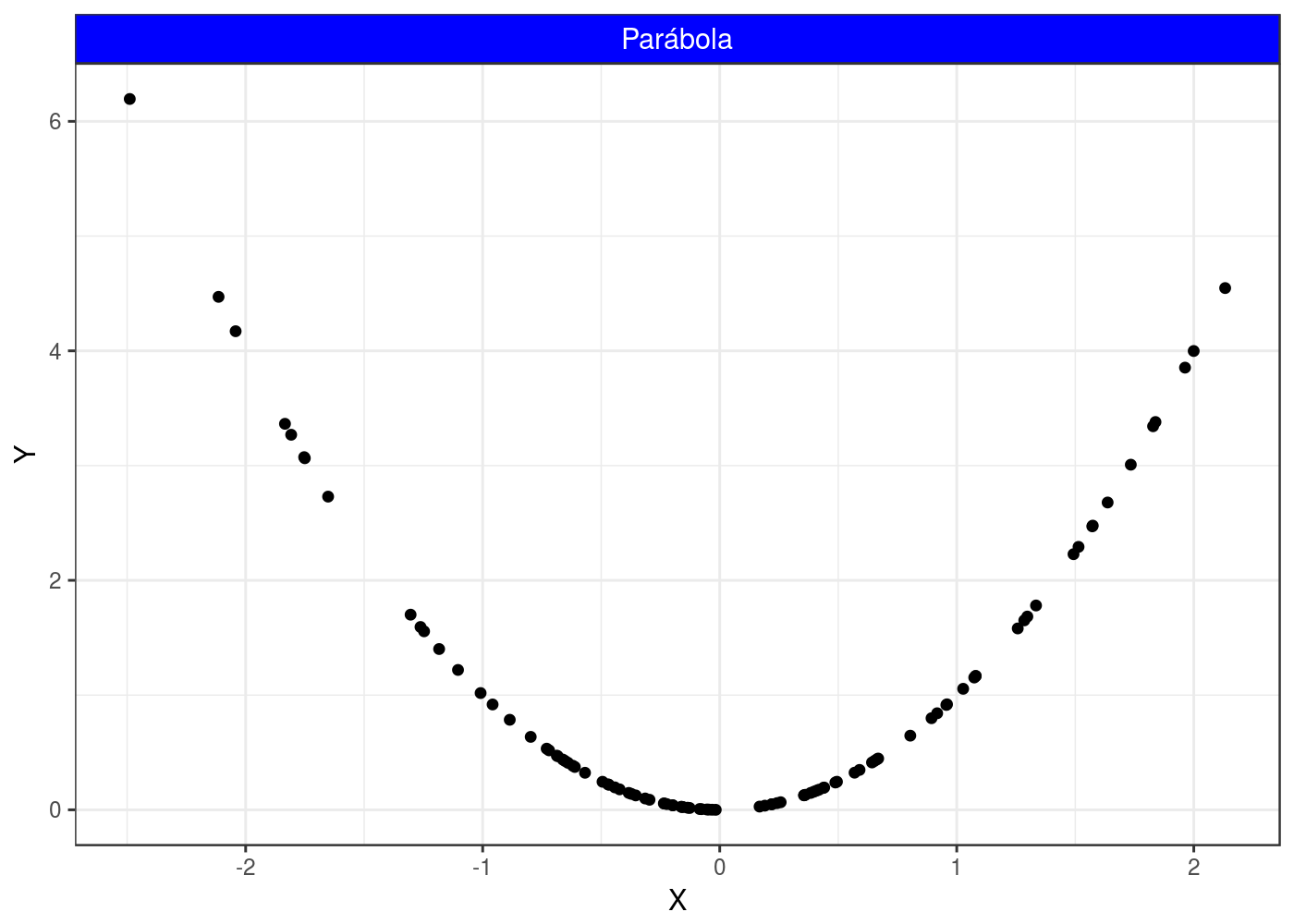
Este gráfico foi colocado propositalmente, pois nota-se claramente que existe uma relação entre as variáveis Y e X, só que a relação não parece com o formato de uma reta, mas sim, com o formato de uma parábola, e assim, o coeficiente de correlação não é indicado para medir essa correlação, e por curiosidade, a correlação resultante foi igual a 0. Para isso, existem outros procedimentos estatísticos capazes de resolver tal situação, tal como a seção aplicação da Tweedie em modelos GAM que foi apresentada nesse post.
Até aqui, falamos somente da correlação. Outro procedimento comum, é testar se a correlação encontrada foi de fato significativa. Para isso, se estabelece as seguinte hipóteses:
\[\left\{\begin{matrix} H_{0}: r = 0\\ vs \\ H_{a}: r \neq 0 \end{matrix}\right.\]
a hipótese \(H_{0}\) indica que não existe correlação entre as duas variáveis, já a \(H{a}\) indica que a correlação não é igual a zero, isto é, testa-se se o coeficiente de correlação é igual ou diferente do zero. Valor-p < 0,05 indica que tais variáveis estão correlacionadas.
Tamanho amostral
Além do próprio coeficiente de correlação, tal teste depende e muito do tamanho amostral. Vamos supor que tivéssemos uma amostra de 1.000.000: mesmo que a correlação entre duas variáveis fosse igual a 0.1, poderíamos ter uma correlação significativa e diferente de 0 por conta do tamanho amostral. Por outro lado, para uma amostra pequena, uma coeficiente significativo indica que de fato tais variáveis podem estar correlacionadas.
Correlação x causa e correlação espúria
É importante destacar também, que correlação não indica causa, apenas mostra que tais variáveis estão correlacionadas. Para concluir que existe causa, é necessário uma análise mais profunda e do estudo de outros fatores que podem influenciar a variável resposta. Uma alta correlação para duas variáveis que de fato não estão correlacionadas é chamada de correlação espúria. O seguinte endereço http://www.tylervigen.com/spurious-correlations apresentam várias variáveis que têm um alto valor de correlação, mas que não estão relacionadas, como por exemplo, número de pessoas que se afogaram numa piscina, e número de filmes que Nicolas Cage atuou.
Demais coeficientes de correlação
Existem outros coeficientes de correlação, como o de Spearman, que é utilizado quando uma variável tem escala ordinal, mas a ideia é a mesma do coeficiente já apresentado. Quando se tem variáveis categóricas, é indicado o coeficiente de contingência C. Todos os coeficientes podem ser encontrados em SIEGEL (1975).
É isso aí pessoal!! Ótima pesquisa!!
Referências
CALLEGARI-JACQUES, S. M. Bioestatística: princípios e aplicações. Traducao. [s.l.] Artmed Editora, 2009.
SIEGEL, S. Estatística não-paramétrica para as ciências do comportamento. Traducao. [s.l.] McGraw-Hill São Paulo, 1975.

