[Guilherme Parreira] | May 16, 2018
Introdução
A curva ROC é uma técnica estatística utilizada principalmente na área da saúde. Basicamente, ela é utilizada para categorizar uma variável numérica X em relação a uma variável categórica Y. Por exemplo, pode ser utilizada para categorizar a idade dos pacientes em relação ao risco de ter a doença de Alzheimer de forma que se tenha uma alocação ótima dos dois grupos de pacientes (com e sem a doença).
Outra aplicação frequente, é após o ajuste de um modelo de regressão logística, em que se tem o interesse de saber se os pacientes tem ou não certa doença. Nesse caso, utiliza-se o valor da probabilidade do paciente apresentar ou não a doença, para ter a melhor separação possível entre o grupo que de fato teve ou não a doença.
Repare que nos dois exemplos apresentados, tem uma variável numérica (no 1º foi a idade, no 2º a probabilidade, que varia de 0 a 1) e deseja-se obter a melhor particão dessas variáveis em termos de uma 2ª variável com 2 categorias (em ambos, ter ou não a doença).
Como quase tudo em estatística, ao categorizar uma variável numérica, normalmente ocorre perda de informação, e nesse caso não é diferente. As classificações geradas pela curva ROC não são perfeitas, isto é, normalmente ocorre erro na classificação dos pacientes. Para isso, são calculadas medidas de qualidade do ajuste da curva ROC para avaliar quão bom foi a categorização de uma variável numérica em termos de uma variável categórica.
Mãos a obra
Para exemplificar a curva ROC, foi criado um conjunto de dados, com apenas 11 pacientes em que foram recordados as informações de idade e se possuíam ou não Alzheimer, conforme tabela sequente:
| Idade | Alzheimer |
|---|---|
| 54 | Não |
| 62 | Não |
| 73 | Não |
| 70 | Sim |
| 48 | Não |
| 101 | Sim |
| 83 | Sim |
| 64 | Sim |
| 96 | Não |
| 67 | Não |
| 61 | Não |
Os pacientes classificados como “Não” referem-se aqueles que não possuem a doença. Já os quais foram classificados como “Sim”, são portadores da doença. Nota-se que 1 paciente com 96 anos não teve Alzheimer e por outro lado, um paciente com 64 teve: tais resultados são menos comuns na prática. No entanto, vale lembrar que interpretações como “à medida que aumenta a idade do paciente, aumenta o risco do paciente vir a ter a doença de Alzheimer” são feitas em relação a maioria(média) da população. Além do mais, essas interpretações não implicam em causa, mas somente em associação.
Procedimento da curva ROC
A curva ROC busca encontrar qual é o valor de idade que classifique os pacientes com e sem a doença da forma que tenha um maior número de acertos na classificação. Para isso, ela avalia todos os pontos de corte possíveis (que referem-se a valores intermediários não observados de idade, nesse caso, seriam 51, 57, … , 101) para a variável idade e para cada um desses valores, se o paciente tem a idade acima da idade do ponto de corte, classifica-o como portador da doença, caso contrário sem a doença. Tal procedimento é repetido para todos os pontos de corte, e avalia-se qual foi o melhor ponto de corte (aquele que proporciona a melhor separação). O que é o melhor ponto de corte é algo que vale a pena uma discussão. Mas por hora, será utilizado o ponto de corte que maximiza a sensibilidade e especificidade, que é a opção padrão dos pacotes estatísticos (pelo menos do pROC).
Medidas de Qualidade do ajuste da curva ROC:
Na sequência é apresentado os conceitos da qualidade de ajuste da curva ROC:
Área abaixo da curva (Area under the curve): Representa a probabilidade de que a curva ROC irá classificar um paciente corretamente. Ela varia de 0 a 1: 0.5 representa um modelo que seria completamente aleatório, ou seja, equivale a decidir se o paciente tem a doença a partir do resultado do lançamento de uma moeda. Quanto mais próximo de 1, e consequentemente longe de 0.5, melhor o ajuste da curva ROC;
Acurácia: Taxa de acertos do modelo: Número de acertos do modelo (seja classificando corretamente os pacientes que apresentaram a doença ou que não apresentaram a doença) divido pelo número de pacientes. Varia de 0 a 1 (Espera-se valores maiores que 0.5);
Sensibilidade: Taxa de verdadeiros positivos: Proporção daqueles que foram classificados pelo modelo com a doença, dado que eles de fato apresentaram a doença. Varia de 0 a 1 (Espera-se valores maiores que 0.5);
Especificidade: Taxa de verdadeiros negativos: Proporção daqueles que foram classificados pelo modelo sem a doença, dado que eles de fato não apresentaram a doença (Espera-se valores maiores que 0.5);
Taxa de Falsos positivos: Proporção de pacientes que foram classificados pelo modelo com a doença, dado que eles não apresentam a doença (Espera-se valores menores que 0.5). Equivale a 1−Especificidade;
Taxa de Falso negativos: Proporção de pacientes que foram classificados sem a doença, dado que eles de fato apresentam a doença (Espera-se valores menores que 0.5). Equivale a 1−Sensibilidade;
Nota-se que as 4 primeiras medidas discriminam o quanto a escolha do ponto de corte foi adequada, enquanto que as duas últimas discriminam o quanto a escolha do ponto de corte foi inadequada.
A próxima tabela apresenta todos os pontos de corte, bem como os respectivos valores de especificidade, sensibilidade e da soma de ambos (para a escolha do ponto de corte ótimo):
| P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 | P10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Ponto de Corte | 51.0 | 57.5 | 61.5 | 63.0 | 65.5 | 68.5 | 71.5 | 78.0 | 89.5 | 98.5 |
| Especificidade (E) | 14.3 | 28.6 | 42.9 | 57.1 | 57.1 | 71.4 | 71.4 | 85.7 | 85.7 | 100.0 |
| Sensibilidade (S) | 100.0 | 100.0 | 100.0 | 100.0 | 75.0 | 75.0 | 50.0 | 50.0 | 25.0 | 25.0 |
| E + S | 114.3 | 128.6 | 142.9 | 157.1 | 132.1 | 146.4 | 121.4 | 135.7 | 110.7 | 125.0 |
Ao escolher um ponto de corte igual a 51 anos, pacientes acima de 51 anos são considerados portadores da doença, e abaixo não são considerados. Como resultado, todos os pacientes que tem a doença de Alzheimer, foram classificados corretamente pela curva ROC. Por outro lado, apenas 14.29% dos pacientes que não tem a doença, foram classificados como não tendo a doença. O conjunto de dados fica da seguinte forma:
| Idade | Alzheimer | Alzheimer Curva ROC |
|---|---|---|
| 54 | Não | Sim |
| 62 | Não | Sim |
| 73 | Não | Sim |
| 70 | Sim | Sim |
| 48 | Não | Não |
| 101 | Sim | Sim |
| 83 | Sim | Sim |
| 64 | Sim | Sim |
| 96 | Não | Sim |
| 67 | Não | Sim |
| 61 | Não | Sim |
| Alzheimer Curva ROC | Não | Sim | Total linha |
|---|---|---|---|
| Não | 1 ; (14.3%) | 0 ; (0%) | 1 ; (9.1%) |
| Sim | 6 ; (85.7%) | 4 ; (100%) | 10 ; (90.9%) |
| Total Coluna (100%) | 7 ; (100%) | 4 ; (100%) | 11 |
Dessa forma, é mais simples de entender como foram calculadas todas as medidas. Dos 7 pacientes que não tinham Alzheimer, apenas 1 a curva ROC classificou corretamente como não tendo Alzheimer: todos os outros 6 pacientes foram classificados com a doença. Por outro lado, dos 4 pacientes que tinham o Alzheimer, os 4 foram classificados como portadores de Alzheimer.
A especificidade e sensibilidade foram calculadas respeitando o total coluna:
Especificidade=17=14.3%
Sensibilidade=44=100%
e ainda, podemos calcular a acurácia: Acurácia=511=45.5%.
Note que a escolha desse ponto de corte produz medidas de qualidade muito pobres (performa pior que se utilizasse uma moeda para decidir se o paciente tem ou não a doença, uma vez que a acurácia foi menor que 50%).
No entanto, essa não foi a escolha ótima para o ponto de corte, mas sim o ponto de corte igual a 63, pois teve o maior valor de sensibilidade e especificidade de forma conjunta. O resultado final da classificação da curva ROC a partir da escolha ótima do ponto de corte é apresentada a seguir:
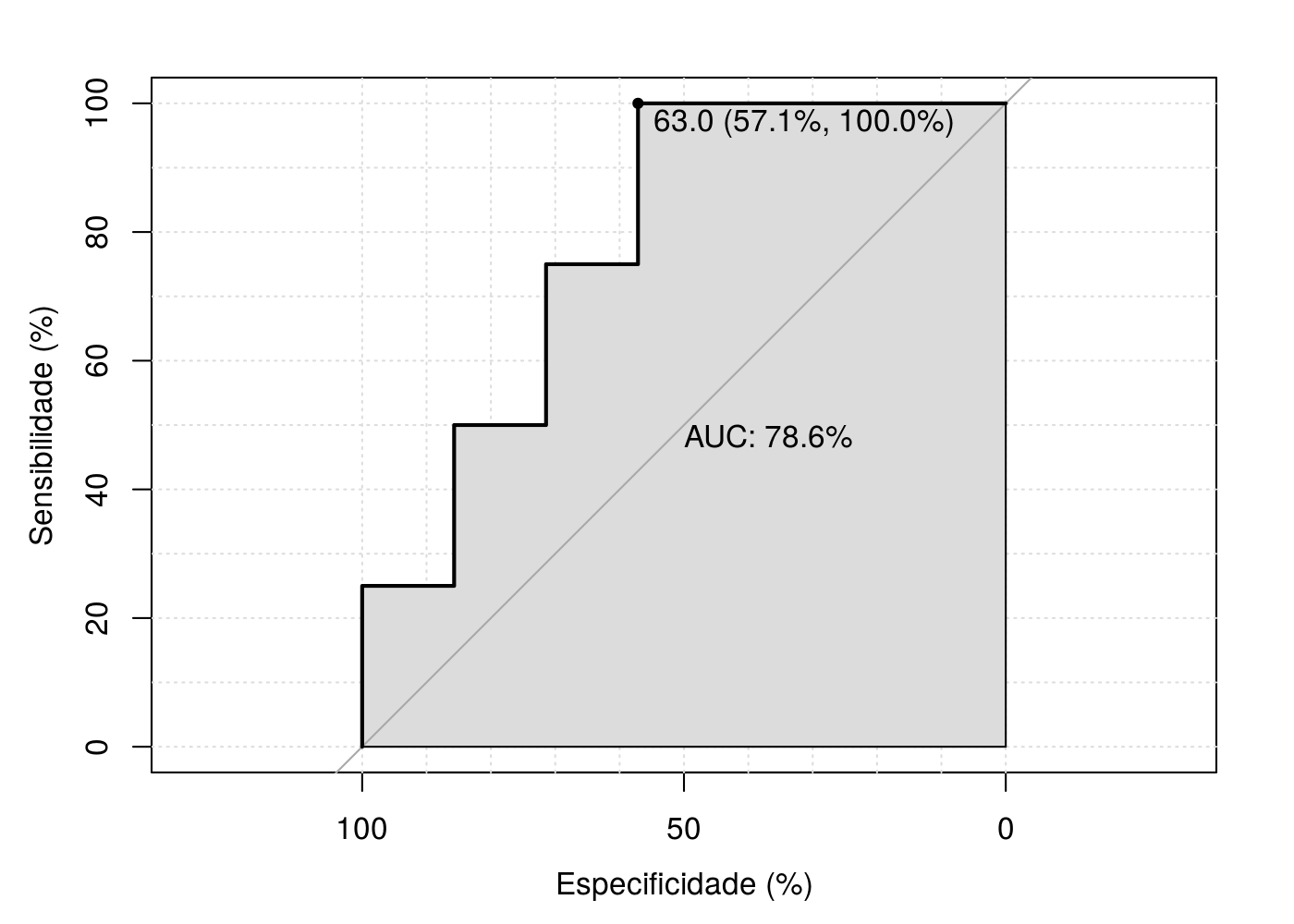
Essa é uma representação clássica da curva ROC. No eixo Y apresenta-se os valores da sensibilidade, no eixo x os valores de especificidade. A linha na diagonal representa a classificação da curva ROC, caso ela fosse feita de maneira aleatório. Quanto mais a extrema esquerda tiver o ponto de corte escolhido, maior será a especificidade e sensibilidade. Da mesma forma, quanto maior for a área em cinza (e acima da linha diagonal) melhor será a estratificação das categorias, e consequentemente maior o valor da área abaixo da curva AUC.
Nesse caso, o ponto de corte escolhido foi igual a 63 (e está representado antes do parêntesis), em seguida, é apresentado a especificidade (57.1%) e a sensibilidade (100%). As demais quebras (formato de escada) no canto superior esquerda da área em cinza representa os diferentes pontos de corte encontrados e já apresentados aqui.
A tabela cruzada para esse ponto de corte á apresentado a seguir:
| Alzheimer Curva ROC | Não | Sim | Total linha |
|---|---|---|---|
| Não | 4 ; (57.1%) | 0 ; (0%) | 4 ; (36.4%) |
| Sim | 3 ; (42.9%) | 4 ; (100%) | 7 ; (63.6%) |
| Total Coluna (100%) | 7 ; (100%) | 4 ; (100%) | 11 |
De um modo geral a curva ROC conseguiu classificar corretamente todos aqueles pacientes que possuíam o Alzheimer, mas não aqueles que não possuíam. Ou ainda, se olhar por outro ângulo, caso o modelo classifique um paciente sem ter o Alzheimer, podemos ficar tranquilos, pois ele não errou nenhuma classificação; no entanto, se o modelo classificar algum paciente tendo o Alzheimer, seria necessário fazer um 2º exame para avaliar se de fato o paciente tem a doença, pois dos 7 pacientes classificados com o Alzheimer, apenas 4 de fato tinham a doença.
Reflexão sobre o “melhor ponto de corte”
Como havia comentando no começo do texto, o conceito do melhor ponto de corte é algo relativo. Nesse caso, o que é melhor (ou menos pior):
- Falar que uma pessoa tem a doença quando ela não tem a doença; Ou:
- Falar que a pessoa não tem a doença quando ela de fato tem a doença;
Nesses caso, é sempre válido o pesquisador ter uma ideia clara do problema para poder fazer a melhor escolha. A resposta a pergunta acima normalmente leva em conta critérios financeiros, ou mesmo o bem estar da sociedade em geral.
O ponto de corte “ótimo” teve um baixo valor de especificidade (57%). O segundo “melhor” ponto de corte (P6), teve uma especificidade de 71.4% e sensibilidade de 75%. Note que a sensibilidade piorou, no entanto a especificidade aumentou: ou seja, a escolha desse ponto de corte implica que dentre as pessoas que não tinham a doença, o ajuste pela curva ROC passou a acertar mais; por outro lado, dentre as pessoas que tem a doença, o ajuste da curva ROC diminuiu o percentual de acertos.
Segue a tabela de dupla entrada (tabela cruzada):
| Alzheimer Curva ROC - P6 | Não | Sim | Total linha |
|---|---|---|---|
| Não | 5 ; (71.4%) | 1 ; (25%) | 6 ; (54.5%) |
| Sim | 2 ; (28.6%) | 3 ; (75%) | 5 ; (45.5%) |
| Total Coluna (100%) | 7 ; (100%) | 4 ; (100%) | 11 |
Nesse caso, vê-se uma proporção mais equilibrada de acertos para ambos os grupos. Entre os 6 pacientes que o modelo classificou como não sendo portadores da doença, 5 (83.3%) foram classificados corretamente; entre os 5 pacientes que o modelo classificou como portadores da doença, 3 (60%) foram classificados corretamente.
Curva ROC para variável com mais que duas categorias
A curva ROC foi criada especialmente quando se tem uma variável resposta com duas categorias, e outra numérica. Quando se tem uma variável resposta com mais que 2 categorias, o que normalmente é utilizado, porém não é uma convenção, é comparar todas as categorias contra uma única categoria. No entanto, isso já é assunto para outro tópico!
Até mais pessoal! Boa pesquisa!

