[Guilherme Parreira] | May 15, 2018
Olá pessoal, tudo bem?
Hoje irei tratar de um gráfico bem comum na análise de dados: o gráfico boxplot, também conhecido como whiskers and tail (BUSSAB; MORETTIN, 2010).
Quando se tem uma variável que seja numérica e busca-se resumir ela a partir de medidas descritivas, um dos gráficos mais comuns é o boxplot. Pois ele permite visualizar a distribuição de uma variável em termos da sua locação (mediana/quartis), dispersão (variabilidade), grau de assimetria, presença de valores extremos/discrepantes (outliers), entre outros.
O gráfico boxplot é puramente descritivo, e utiliza-se de medidas descritivas, mais especificamente dos quartis e do intervalo interquatil (IIQ) na construção do gráfico:
- \(Q_{1}\) (1º quartil): Identifica que, 25% das observações estão abaixo do valor de \(Q_{1}\). Ele é representado pela linha inferior da caixa do boxplot;
- \(Q_{2}\) (2º quartil): Identifica que, 50% das observações estão abaixo e acima do valor de \(Q_{2}\). Mais conhecida como mediana. Ele é representado pela linha do meio da caixa e mais espessa.
- \(Q_{3}\) (3º quartil): Identifica que, 75% das observações estão abaixo do valor de \(Q_{3}\). Ele é representado pela linha superior da caixa do boxplot;
- O intervalo interquatil (IIQ) é calculado por \(Q_{3}-Q_{1}\);
- Os outliers são os valores que estão abaixo de \(Q_{1} -1.5*IIQ\) e acima de \(Q_{3} + 1.5*IIQ\) e são representados por pontos no gráfico. Ou seja, são mensurações cuja a maioria do conjunto de dados não segue o mesmo padrão;
- A haste inferior é o valor mínimo da amostra removendo-se os outliers;
- A haste superior é o valor máximo da amostra removendo-se os outliers;
O desvio \(1.5*IIQ\), é calculado de tal forma que espera-se que todos os dados estejam dentro desses limites, valores fora, representam outliers. Lembrando que, se os dados são simétricos, então a média é igual a mediana, e o tamanho da caixa é divido ao meio, ou seja, formando dois retângulos de mesmo tamanho e hastes com o mesmo comprimento.
Para exemplificar o gráfico boxplot, foram criados dados da altura dos moradores de uma cidade qualquer, e deseja-se fazer um resumo dessas alturas a partir do gráfico boxplot. A próxima figura é a representação clássica do gráfico boxplot para a altura dos moradores proposto por John Tukey (1969):
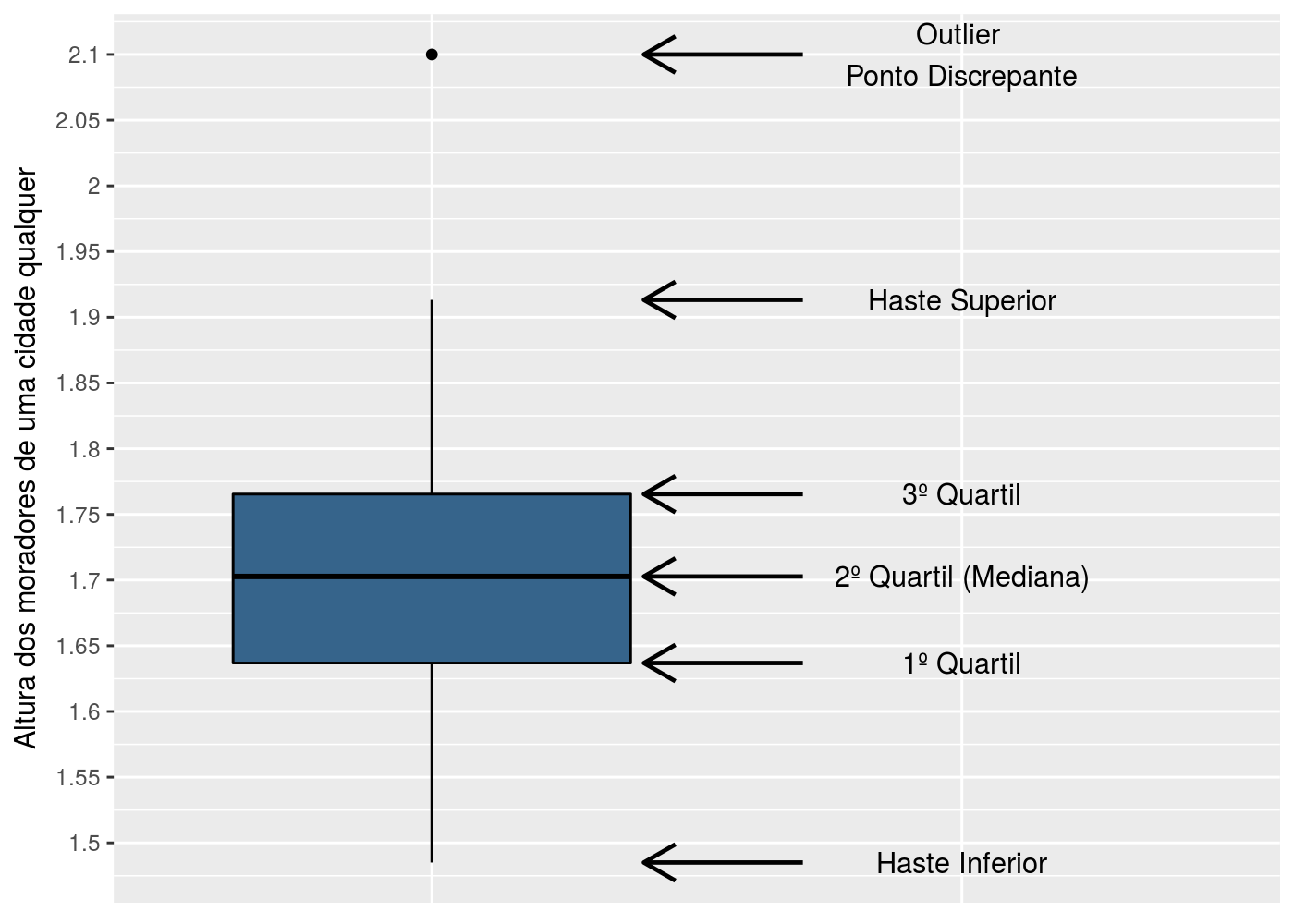
Nesse caso a mediana da altura dos cidadãos foi próxima de 1.7, 1º Quartil próximo de 1.63, 3º Quartil próximo de 1.77. As hastes inferiores e superiores foram próximos de 1.48 e 1.92. O outlier representado pelo gráfico foi igual a 2,10m, ou seja, não foi uma altura muito comum nos dados criados, e também faz sentido na prática (embora não seja um conjunto de dados real), pois não é comum pessoas tão altas na sociedade.
A vantagem de se utilizar ele ao invés de uma tabela descritiva (com média, desvio padrão, mediana, etc…), é que é possível visualizar a distribuição dos dados rapidamente, sem precisar olhar especificamente para cada dado do seu conjunto de dados, que é uma tarefa inviável.
Essa é a construção padrão de um gráfico boxplot. Outras modificações foram sugeridas por diferentes autores e implementadas por diferentes pacotes estatísticos, e são exibidas na sequência.
Largura da caixa proporcional ao tamanho amostral
A partir da biblioteca de gráficos ggplot2 (WICKHAM, 2009), que está disponível no software estatístico R (R CORE TEAM, 2018), é possível fazer a largura da caixa do boxplot proporcional a raiz quadrada do número de observações em cada grupo.
Para isso, foram criados dados da altura de pessoas do sexo masculino e do sexo feminino só que com tamanhos amostrais diferentes: 51 para o sexo masculino e 150 para o sexo feminino. Nesse exemplo é útil utilizar tal recurso dado o desbalanceamento dos grupos. Nesse caso, o tamanho da caixa para o sexo masculino em relação ao do sexo feminino é de: \[\frac{\sqrt{51}}{\sqrt{150}} = \frac{7.14}{12.247} = 58.31\%.\] Os desenvolvedores do pacote utilizaram a transformação da raiz quadrada para diminuir o efeito da diferença do tamanho amostral, caso contrário, teria que se fazer uma caixa 3x maior que a outra. Essa diferença é representada no gráfico a seguir:
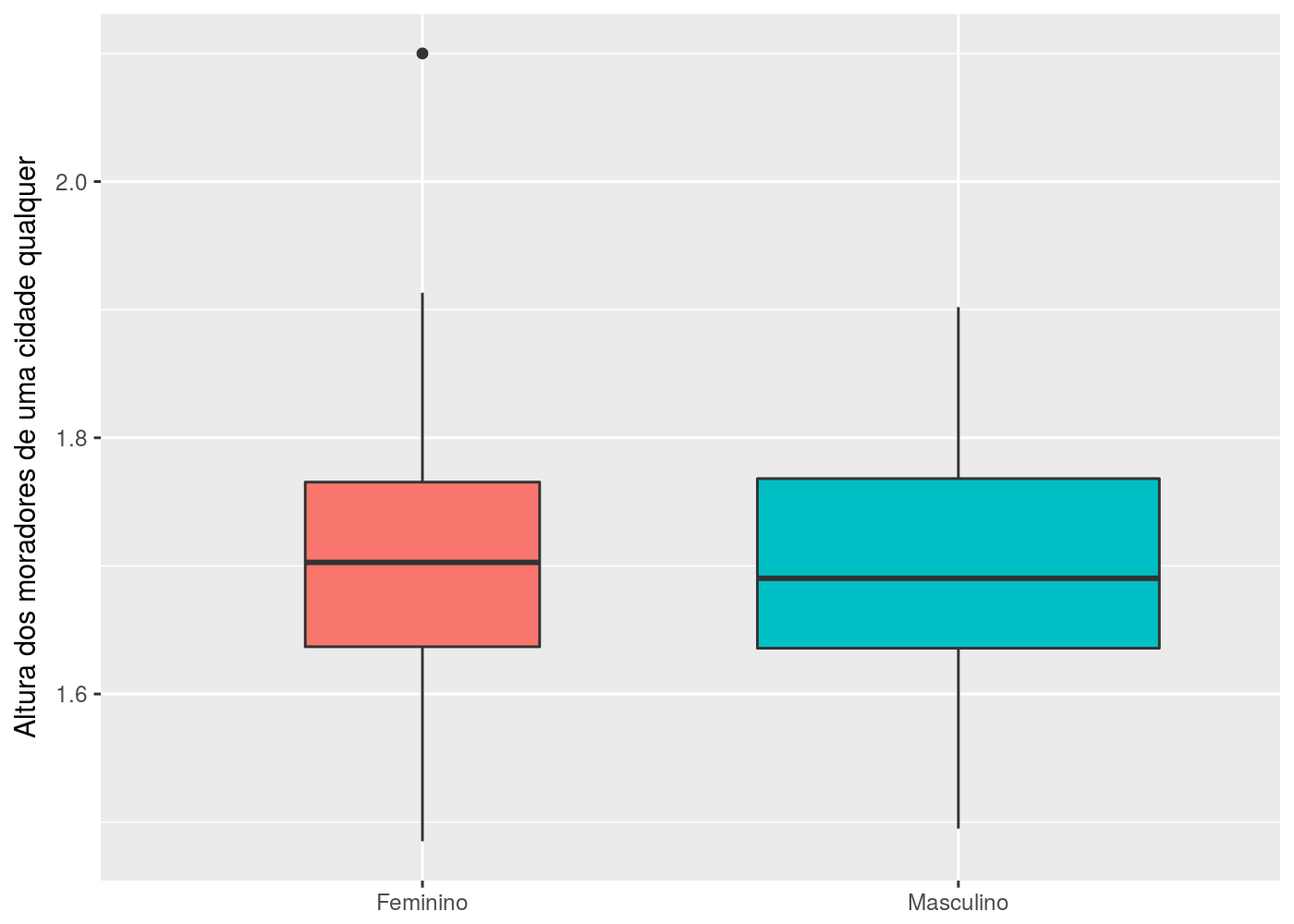
Caso tenha ficado com dúvida sobre como a largura do boxplot foi determinada, a partir de uma régua, é possível medir a largura da caixa para o sexo feminino e dividir pela largura da caixa para o sexo masculino. O resultado será próximo de 58%. Nesse caso, a figura mostra que a amostra para o sexo feminino foi menor que a do sexo masculino.
Com pontos
Uma outra facilidade, é adicionar as alturas que de fato foram observadas os indivíduos:
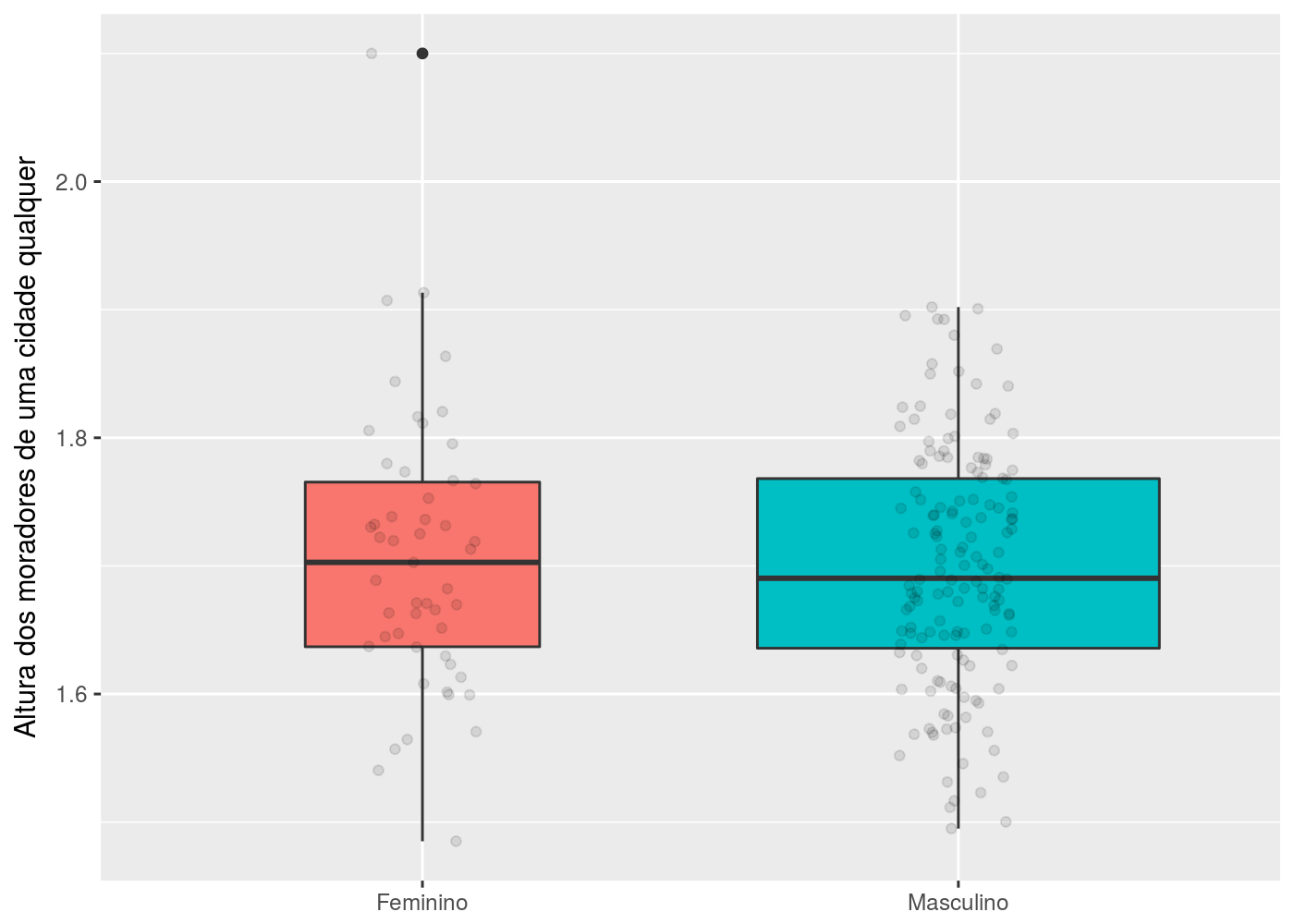
Os pontos vazados e mais claros mostram os dados observados em si. Para ser possível visualizar todos os dados foi necessário adicionar um pequeno jitter no eixo “x”, caso contrário, todos os pontos ficariam sobrepostos.
Boxplot + Violino
Ainda, é possível adicionar um “violino” ao gráfico boxplot:
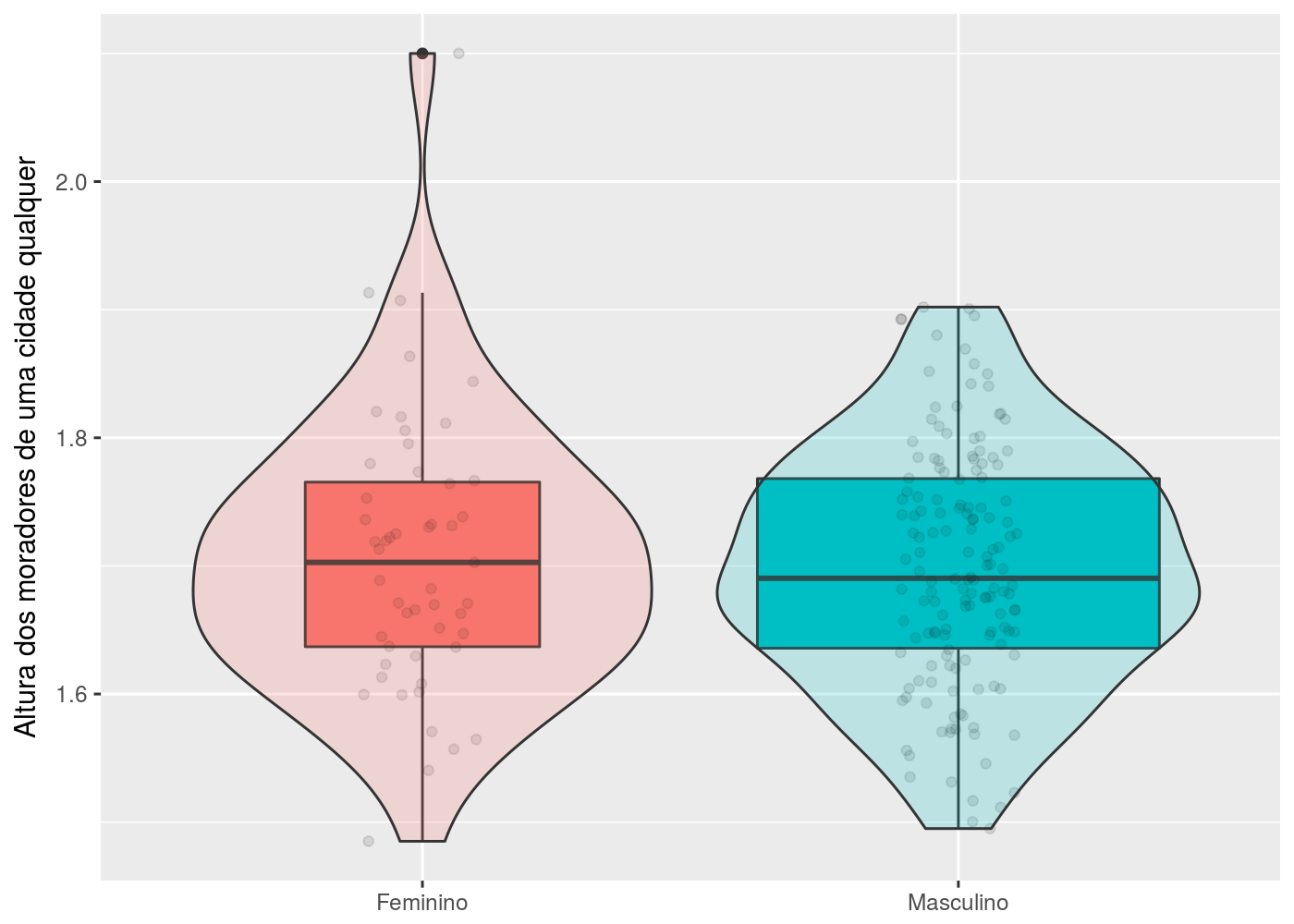
O “violino” são as curvas no entorno do gráfico boxplot, e representa a função densidade de probabilidade estimada via kernel (basicamente, as curvas mais largas representam maior densidade de pontos, ou seja, existe uma maior frequência de pontos). Esse tipo de representação pode ser útil para alguns conjuntos de dados, pois pelo fato do boxplot resumir os dados em 5 medidas descritivas, pode haver perda de informação. Já o “violino” resume os dados em uma função densidade, caracterizando melhor o conjunto de dados. Note que para os indivíduos do sexo masculino, a forma do violino (densidade de pontos) é um pouco mais larga abaixo da mediana. Já para os indivíduos do sexo feminino, a forma do violino está bem “arrendondada”/densa no entorno da mediana. Ou seja, os indivíduos do sexo feminino tiveram alturas levemente superiores as dos indivíduos do sexo masculino (bem levemente superior).
Todos os boxplots apresentados até que foram “bem comportados”, isto é:
- A distância entre o \(Q_{1}\) e a mediana foi similar a distância entre a mediana e o \(Q_{3}\);
- Os dados mostraram poucos outliers;
- Ambos grupos variaram de forma parecida;
- A locação (mediana/quartis) de ambos grupos estavam próximas.
Agora, irei apresentar alguns boxplots cujos comportamentos dos mesmos não estão “bem comportados”. Digo “bem comportados”, uma vez que a distribuição dos boxplots e do violino, assemelha-se de uma distribuição Normal.
Alta dispersão em um grupo
Para representar maior dispersão em um dos grupos, foi criado um conjunto de dados referente ao peso de recém-nascidos para cada sexo. Os mesmos são mostrados no próximo gráfico:
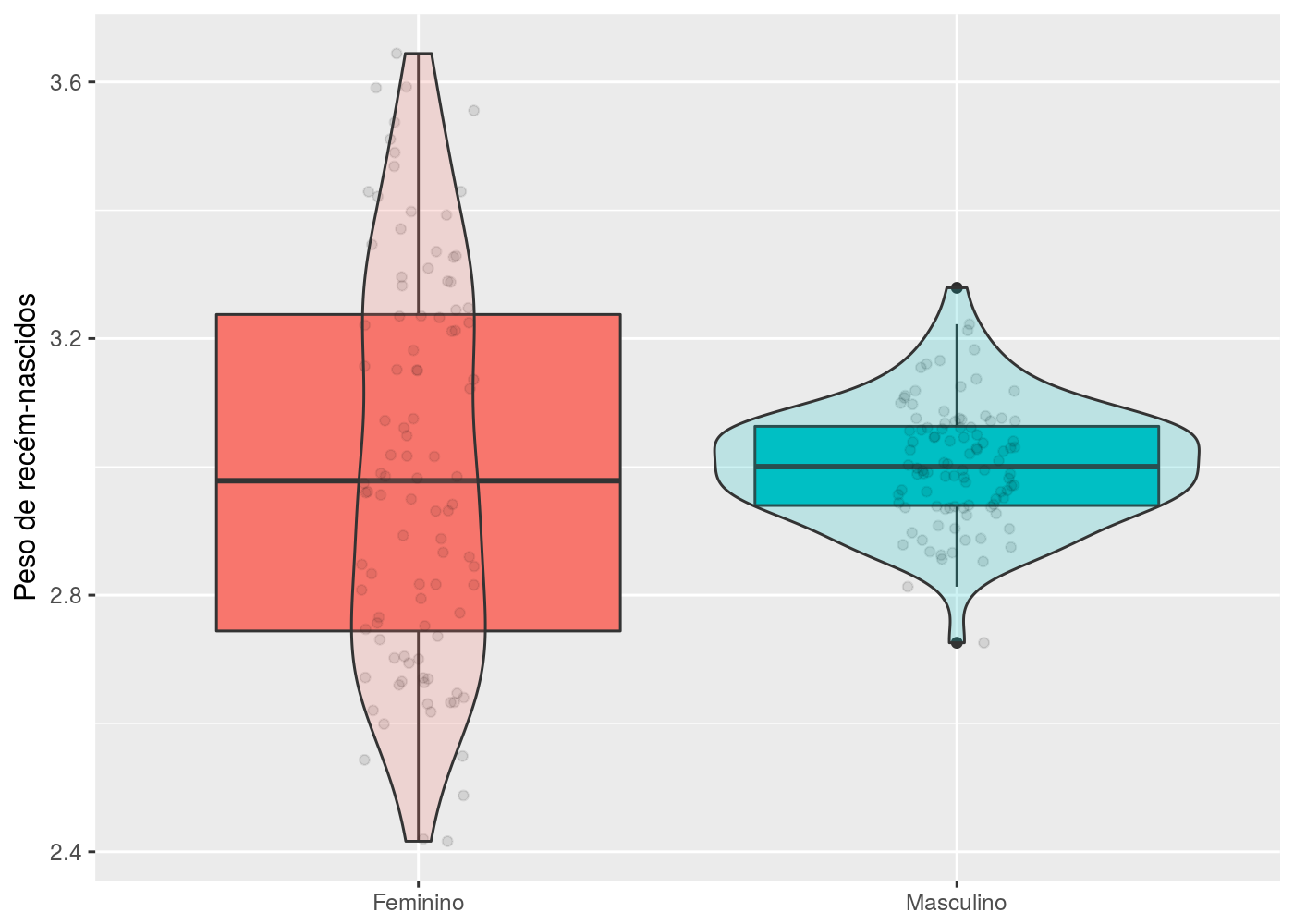
Nota-se que os recém-nascidos do sexo feminino variaram de cerca de 2.4kg até 3.6kg; enquanto que os recém-nascidos do sexo masculino variaram por cerca de 2.8kg até 3.2kg. Embora a variabilidade dos recém-nascidos do sexo feminino foi bem maior que os do sexo masculino, a locação dos dados (média/quartis) foi similar entre os grupos.
Grupos com médias diferentes e alta dispersão em um grupo
Aqui, foram mantidos os mesmos dados do gráfico anterior para o sexo feminino, e para o sexo masculino foi adicionado 0.3kg ao peso de cada recém-nascido:
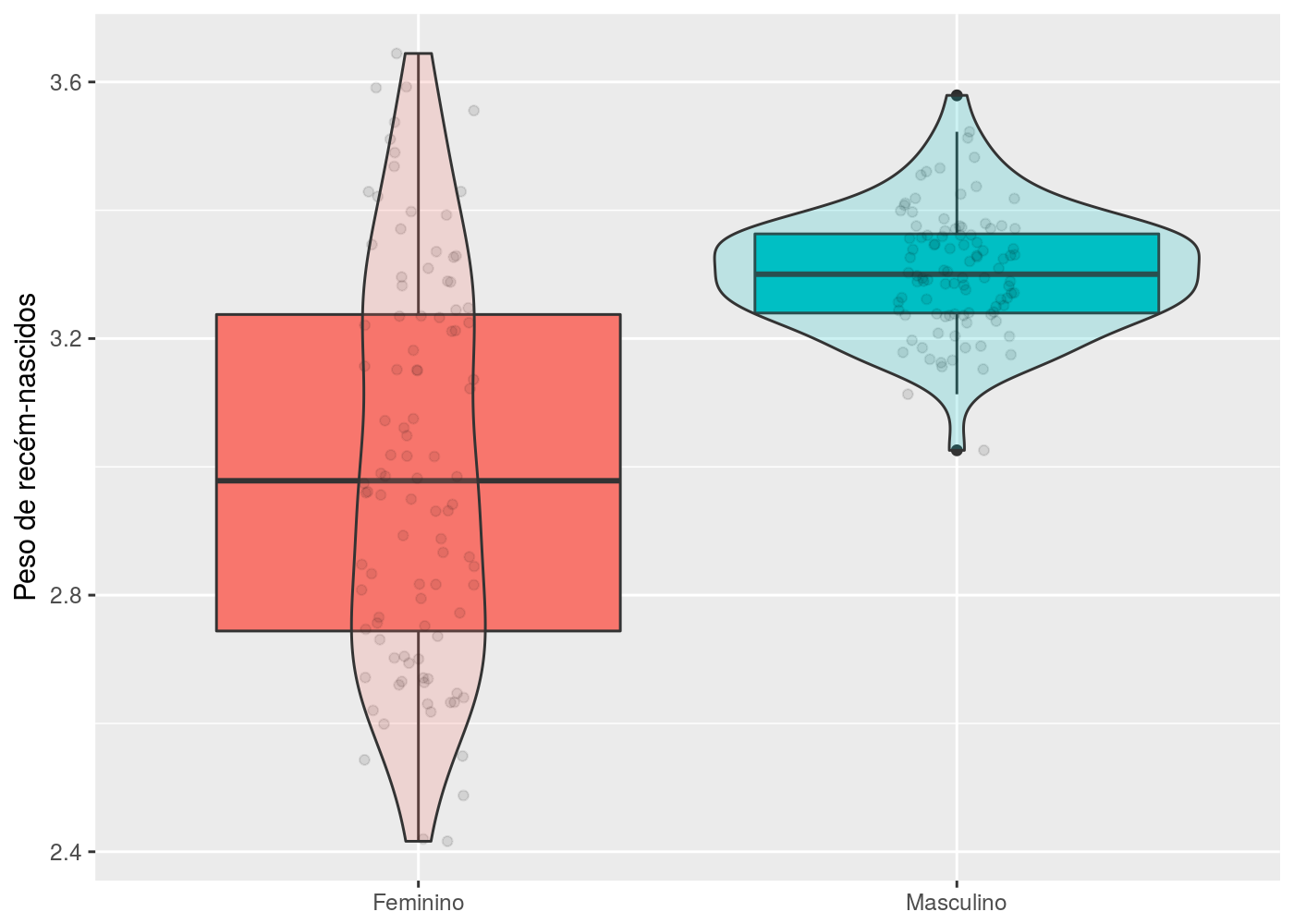
Fica claro que os recém-nascidos do sexo masculino tiveram maior peso que os recém-nascidos do sexo feminino, além de uma menor variabilidade.
Grupo com assimetria à direita
Aqui, continuamos com a mesma representação para o peso dos recém-nascidos para o sexo masculino, mas para o sexo feminino, vamos supor que (embora isso não ocorra na prática) existe um maior número de recém-nascidos do sexo feminino com sobrepeso. O próximo gráfico ilustra essa situação:
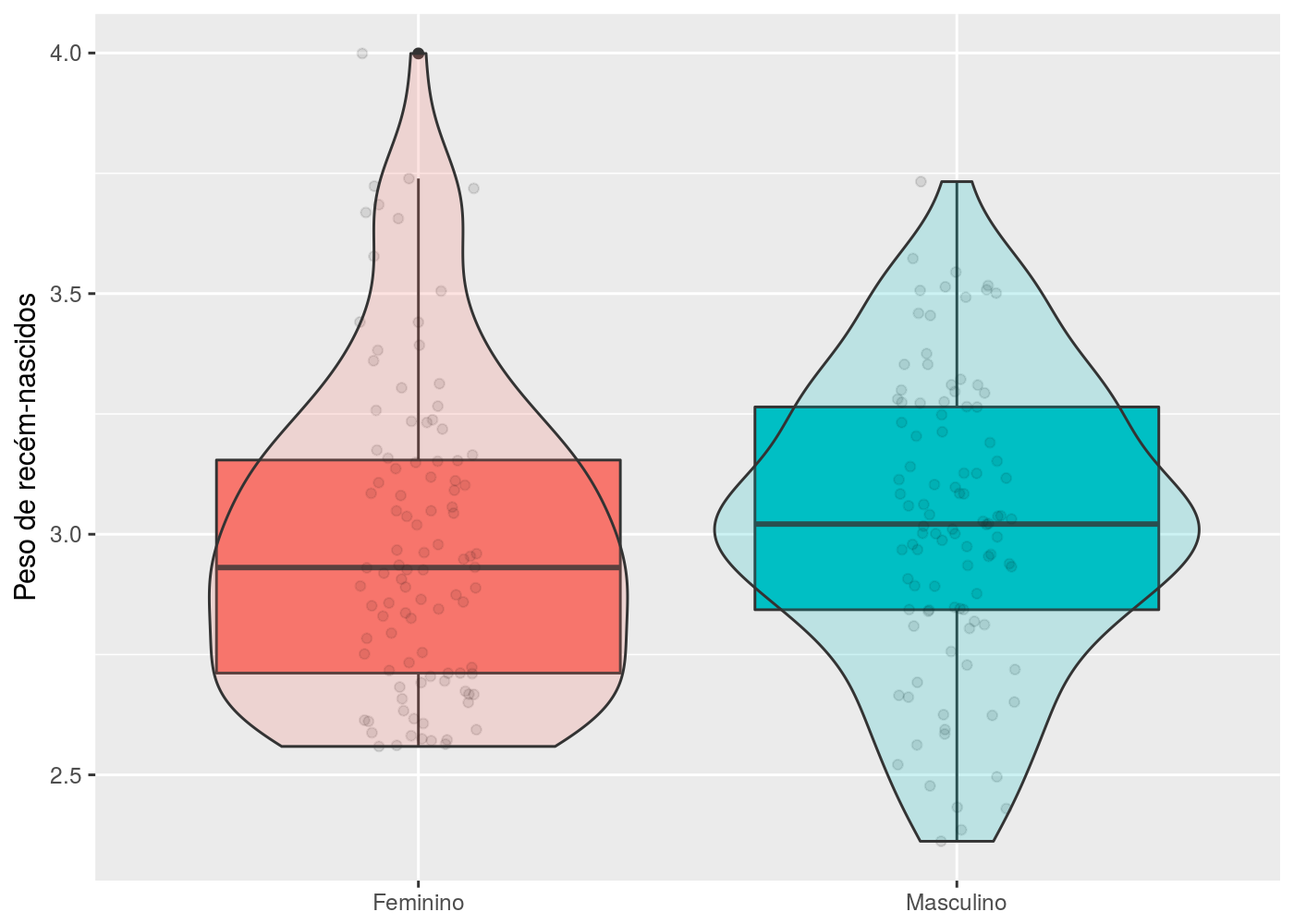
Aqui, como de costume, o peso mediano dos recém-nascidos para o sexo masculino foi igual a 3kg e a variabilidade ao redor da mediana se deu de forma proporcional (tanto acima e abaixo). Já para os recém-nascidos do sexo feminino, nota-se que tiveram recém-nascidos com peso maior que 3.7kg (enquanto não teve recém-nascidos com peso menor que 2.5kg), que é um indicativo de assimetria; ainda, a partir do violino, nota-se uma maior densidade de pontos entre 2.5kg e 3.25kg, e a medida que afasta-se de 3.5kg a densidade de pontos diminui.
É isso pessoal! Espero que tenham aproveitado e aprendido um pouco mais sobre o boxplot.
Ótima pesquisa!
Referências
BUSSAB, W. DE O.; MORETTIN, P. A. Estatística básica. Traducao. [s.l.] Saraiva, 2010.
R CORE TEAM. R: A Language and Environment for Statistical Computing. Traducao. Vienna, Austria: R Foundation for Statistical Computing, 2018.
WICKHAM, H. ggplot2: Elegant Graphics for Data Analysis. Traducao. [s.l.] Springer-Verlag New York, 2009.

